Bài 84 trang 99 sgk Toán lớp 9 tập 2

Bài 84. a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh \(C\) của tam giác đều \(ABC\) cạnh \(1 cm\). Nêu cách vẽ (h.63).

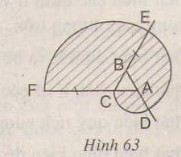
b) Tính diện tích miền gạch sọc.

Hướng dẫn giải:

a) Vẽ tam giác đều \(ABC\) cạnh \(1cm\)

Vẽ \(\frac{1}{3}\) đường tròn tâm \(A\), bán kính \(1cm\), ta được cung \(\overparen{CD}\)

Vẽ \(\frac{1}{3}\) đường tròn tâm \(B\), bán kính \(2cm\), ta được cung \(\overparen{DE}\)

Vẽ \(\frac{1}{3}\) đường tròn tâm \(C\), bán kính \(3cm\), ta được cung \(\overparen{EF}\)

b) Diện tích hình quạt \(CAD\) là \(\frac{1}{3}\) \(π.1^2\)

Diện tích hình quạt \(DBE\) là \(\frac{1}{3}\) \(π.2^2\) 

Diện tích hình quạt \(ECF\) là \(\frac{1}{3}\) \(π.3^2\)

Diện tích phần gạch sọc là  \(\frac{1}{3}\) \(π.1^2\)+ \(\frac{1}{3}\) \(π.2^2\) + \(\frac{1}{3}\) \(π.3^2\)

                                   = \(\frac{1}{3}\) \(π (1^2 + 2^2 + 3^2)\) = \(\frac{14}{3}π\) (\(cm^2\))

Bài 85 trang 100 sgk Toán lớp 9 tập 2

Bài 85. Hình viên phân là hình tròn giới hạn bởi một cung tròn và dây căng cung ấy. Hãy tính diện tích hình viên phân \(AmB\), biết góc ở tâm \(\widehat {AOB} = {60^0}\) và bán kính đường tròn là \(5,1 cm\) (h.64)

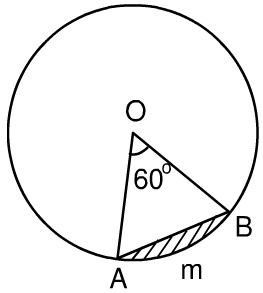
Hướng dẫn giải:

\(∆OAB\) là tam giác đều có cạnh bằng \(R = 5,1cm\). Áp dụng công thức tính diện tích tam giác đều cạnh \(a\) là \({{{a^2}\sqrt 3 } \over 4}\) ta có 

 \({S_{\Delta OBC}} = {{{R^2}\sqrt 3 } \over 4}\)           (1)

Diện tích hình quạt tròn \(AOB\) là:

 \({{\pi .{R^2}{{.60}^0}} \over {{{360}^0}}} = {{\pi {R^2}} \over 6}\)     (2)

Từ (1) và (2) suy ra diện tích hình viên phân là:

\({{\pi {R^2}} \over 6} - {{{R^2}\sqrt 3 } \over 4} = {R^2}\left( {{\pi  \over 6} - {{\sqrt 3 } \over 4}} \right)\)

Thay \(R = 5,1\) ta có \(S\)_{viên phân} ≈\( 2,4\) (\(cm^2\))

Bài 86 trang 100 sgk Toán lớp 9 tập 2

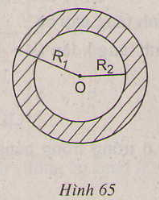
Bài 86. Hình vành khăn là phần hình tròn nằm giữa hai đường tròn đồng tâm (h.65).

a) Tính diện tích \(S\) của hình vành khăn theo \({R_1}\) và \({R_2}\) (giả sử \({R_1}>{R_2}\)).

b) Tính diện tích hình vành khăn khi \({R_1} = 10,5 cm\), \({R_2} = 7,8 cm\).

Hướng dẫn giải:

a) Diện tích hình tròn \((O;{R_1})\) là \({S_1 }\)=\( \pi{R_1}^2\).

Diện tích hình tròn \((O;{R_2})\) là \({S_2 }\)=\( \pi{R_2}^2\).

Diện tích hình vành khăn là:

       \(S = {S_1}– {S_2}\) = \( \pi{R_1}^2\)-\( \pi{R_2}^2\)= \( \pi({R_1}^2-{R_2}^2)\)

b) Thay số: \(S = 3,14. (10,5^2 – 7,8^2) = 155,1\)(\(cm^2\))

Bài 87 trang 100 sgk Toán lớp 9 tập 2

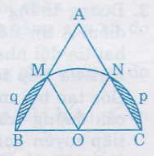
Bài 87. Lấy cạnh \(BC\) của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng \(BC\). Cho biết cạnh \(BC = a\), hãy tính diện tích hình viên phân được tạo thành.

Hướng dẫn giải:

Gọi nửa đường tròn tâm \(O\) đường kính \(BC\) cắt hai cạnh \(AB\) và \(AC\) lần lượt tại \(M\) và \(N\).

\(∆ONC\) có \(OC = ON\), \(\widehat{C}\) = \(60^0\) nên \(∆ONC\) là tam giác đều, do đó \(\widehat{NOC}\) = \(60^0\).

\(S\)_{quạt NOC} = \(\frac{\pi \left ( \frac{a}{2} \right )^{2}.60^{\circ}}{360^{\circ}}\) = \(\frac{\pi a^{2}}{24}\).

\(S\)_∆NOC = \(\frac{\left ( \frac{a}{2} \right )^{2}\sqrt{3}}{4}\) = \(\frac{a^{2}\sqrt{3}}{16}\)

Diện tích hình viên phân: 

\(S\)_CpN  = \(\frac{\pi a^{2}}{24}\) - \(\frac{a^{2}\sqrt{3}}{16}\) = \(\frac{a^{2}}{48}\left ( 2\pi -3\sqrt{3} \right )\)

Vậy diện tích hình viên phhân bên ngoài tam giác là:

            \(\frac{a^{2}}{24}\left ( 2\pi -3\sqrt{3} \right )\)

Giaibaitap.me