Bài 92 trang 104 SGK Toán 9 tập 2

Bài 92. Hãy tính diện tích miền gạch sọc trong các hình 69, 70, 71 (đơn vị độ dài: cm).

Hướng dẫn trả lời:

a) Hình 69

Đối với hình tròn bán kính \(R= 1,5\) là: \({S_1} = πR^2 = π. 1,5^2 = 2,25π\)

Đối với hình tròn bán kính \(r = 1\) là: \({S_2} = πr^2= π. 1^2 = π\)

Vậy diện tích miền gạch sọc là:

\(S = {S_1} – {S_2} = 2,25 π – π = 1,25 π\) (đvdt)

b) Hình 70

Diện tích hình quạt có bán kính \(R = 1,5\); \(n^0 = 80^0\)

\({S_1} = {{\pi {R^2}n} \over {360}} = {{\pi 1,{5^2}.80} \over {360}} = {\pi  \over 2}\) 

Diện tích hình quạt có bán kính \(r = 1\); \(n^0 = 80^0\)

\({S_2} = {{\pi {r^2}n} \over {360}} = {{\pi {{.1}^2}.80} \over {360}} = {{2\pi } \over 9}\)

Vậy diện tích miền gạch sọc là: \(S = {S_1} - {S_2} = {\pi  \over 2} - {{2\pi } \over 9} = {{9\pi  - 4\pi } \over {18}} = {{5\pi } \over {18}}\)

c) Hình 71

Diện tích hình vuông cạnh \(a = 3\) là:

\({S_1} = a^2 = 3^2 =9\)

Diện tích hình tròn có \(R = 1,5\) là:

\({S_2} = πR^2 = π.1,5^2 = 2,25π = 7,06\)

Vậy diện tích miền gạch sọc là:

\(S = {S_1} – {S_2} = 9 – 7,06 = 1,94\) (đvdt).

Bài 93 trang 104 SGK Toán 9 tập 2

Bài 93. Có ba bánh xe răng cưa \(A, B, C\) cùng chuyển độn ăn khớp với nhau. Khi một bánh xe quay thì hai bánh xe còn lại cũng quay theo. Bánh xe \(A\) có \(60\) răng, bánh xe B có \(40\) răng, bánh xe \(C\) có \(20\) răng. Biết bán kính bánh xe \(C\) là \(1\)cm. Hỏi:

a) Khi bánh xe \(C\) quay \(60\) vòng thì bánh xe \(B\) quay mấy vòng?

b) Khi bánh xe \(A\) quay \(80\) vòng thì bánh xe \(B\) quay mấy vòng?

c) Bán kính của các bánh xe \(A\) và \(B\) là bao nhiêu?

Hướng dẫn trả lời:

Ta có bánh xe \(A\) có \(60\) răng, bánh xe \(B\) có \(40\) răng, bánh xe \(C\) có \(20\) răng nên suy ra chu vi của bánh xe \(B\) gấp đôi chu vi bánh xe \(C\), chu vi bánh xe \(A\) gấp ba chu vi bánh xe \(C\).

Chu vi bánh xe \(C\) là: \(2. 3,14 . 1 = 6,28 (cm)\)

Chu vi bánh xe \(B\) là: \(6,28 . 2 = 12,56 (cm)\)

Chu vi bánh xe \(A\) là: \(6,28 . 3 = 18,84 (cm)\)

a) Khi bánh xe \(C\) quay được \(60\) vòng thì quãng đường đi được là:

\(60 . 6,28 = 376,8 (cm)\)

Khi đó số vòng quay của bánh xe \(B\) là:

\(376,8 : 12,56 = 30\) (vòng)

b) Khi bánh xe \(A\) quay được \(80\) vòng thì quãng đường đi được là:

\(80 . 18,84 = 1507,2\) (cm)

Khi đó số vòng quay của bánh xe \(B\) là:

\(1507,2 : 12,56 = 120\) (vòng)

c) Bán kính bánh xe \(B\) là: \(12,56 : (2π) = 12,56 : 6,28 = 2(cm)\)

Bán kính bánh xe \(A\) là: \(18,84 : (2π) = 18,84 : 6,28 = 3(cm)\)

Bài 94 trang 105 SGK Toán 9 tập 2

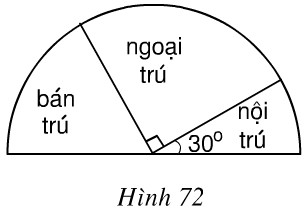
Bài 94. Hãy xem biểu đồ hình quạt biểu diễn sự phân phối học sinh của một trường THCS theo diện ngoại trú, bán trú, nội trú (h.72). Hãy trả lời các câu hỏi sau:

a) Có phải \({1 \over 2}\) số học sinh lầ học sinh ngoại trú không?

b) Có phải \({1 \over 3}\) số học sinh là học sinh bán trú không?

c) Số học sinh nội trú chiếm bao nhiêu phần trăm?

d) Tính số học sinh mỗi loại, biết tổng số học sinh là \(1800\) em.

Hướng dẫn trả lời:

Theo cách biểu diễn dự phân phối học sinh như biểu đồ thì:

a) Đúng \(\left( {{1 \over 2} = 50\% } \right)\)

b) Đúng \(\left( {{1 \over 3} \approx 33,3\% } \right)\) 

c) Số học sinh nội trú chiếm \(100\)% - (\(50\)% + \(33,3\)%) = \(16,7\)%

d) Số học sinh ngoại trú:

\(1800.{1 \over 2} = 900\) (em)

Số học sinh bán trú:

\(1800.{1 \over 3} =600\)(em)

Số học sinh nội trú:

\(1800 – (900 + 600) = 300\) (em)

Bài 95 trang 105 SGK Toán 9 tập 2

Bài 95. Các đường cao hạ từ \(A\) và \(B\) của tam giác \(ABC\) cắt nhau tại \(H\) (góc \(C\) khác \(90^0\)) và cắt đường tròn ngoại tiếp tam giác \(ABC\) lần lượt tại \(D\) và \(E\). Chứng minh rằng:

a) \(CD = CE\) ;     b) \(ΔBHD\) cân ;     c) \(CD = CH\).

Hướng dẫn trả lời:

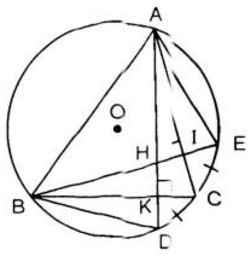
Ta có: \(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}B}\) (cùng chắn cung \(AB\))

 \( \Rightarrow \widehat {CB{\rm{D}}} = \widehat {CA{\rm{E}}}\) (cùng phụ với hai góc bằng nhau)

⇒ \(sđ\overparen{CD}\)= \(sđ\overparen{CE}\)

Suy ra \(CD = CE\)

b) Ta có \(\widehat {EBC}\) và \(\widehat {CB{\rm{D}}}\) là góc nội tiếp trong đường tròn \(O\) nên :

 \(\widehat {EBC} = {1 \over 2} sđ\overparen{CE}\) và \(\widehat {CB{\rm{D}}} = {1 \over 2}sđ\overparen{CD}\) 

Mà \(sđ\overparen{CD}\)= \(sđ\overparen{CE}\)

nên \(\widehat {EBC} = \widehat {CB{\rm{D}}}\)

Vậy \(∆BHD\) cân tại \(B\)

c) Vì \(∆BHD\) cân và \(BK\) là đường cao cũng là đường trung trực của \(HD\). Điểm \(C\) nằm trên đường trung trực của \(HD\) nên \(CH = CD\)

Giaibaitap.me