Bài 81 trang 99 sgk Toán lớp 9 tập 2

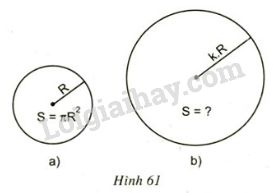
Bài 81. Diện tích hình tròn sẽ thay đổi như thế nào nếu:

a) Bán kính tăng gấp đôi?

b) Bám kinh tăng gấp ba?

c) Bán kính tăng \(k\) lần (\(k>1\))?

Hướng dẫn giải:

Ta có: 

\(π{(2R)}^2 = 4πR^2\)

\(π{(3R)}^2 = 9 πR^2\)

\(π(kR)^2 = k^2 πR^2\)

 Vậy nếu ta gấp đôi bán kính thì diện tích hình tròn sẽ gấp bốn, nếu nhân bán kính với \(k > 0\) thì diện tích hình tròn sẽ gấp \(k^2\) lần.

Bài 82 trang 99 sgk Toán lớp 9 tập 2

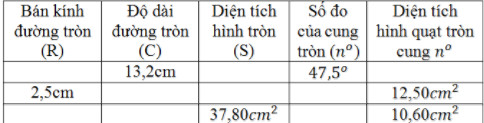
Bài 82. Điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhất)

Giải

- Dòng thứ nhất:

           \( R\) = \(\frac{C}{2\pi }\) = \(\frac{13,2}{2. 3,14 }\) \(≈ 2,1\) (\(cm\))

            \(S = π. R^2 = 3,14.{(2,1)}^2 ≈ 13,8 \)(\(cm^2\))

            \({R_{quạt}}\)= \(\frac{\pi R^{2}n^{\circ}}{360^{\circ}}\) = \(\frac{3,14 .2,1^{2}.47,5}{360}\) \(≈ 1,83\)  (\(cm^2\))

- Dòng thứ hai: \(C = 2πR = 2. 3,14. 2,5 = 15,7\) (cm)

                       \(S = π. R^2 = 3,14.{(2,5)}^2 ≈ 19,6\) (\(cm^2\))

                       \(n^0\) = \(\frac{S_{quat}.360^{\circ}}{\pi R^{2}}\) = \(\frac{12,5.360^{\circ}}{3,14.2,5^{2}}\) \(≈ 229,3^0\)  

- Dòng thứ ba: \(R\) = \(\sqrt{\frac{s}{\pi }}\) = \(\sqrt{\frac{37,8}{3,14 }}\) \(≈ 3,5\) (\(cm\))

                     \(C = 2πR = 22\) (\(cm\))

                      \(n^0\) = \(\frac{S_{quat}.360^{\circ}}{\pi R^{2}}\)= \(\frac{10,6.360^{\circ}}{3,14.3,5^{2}}\) \(≈ 99,2^0\)  

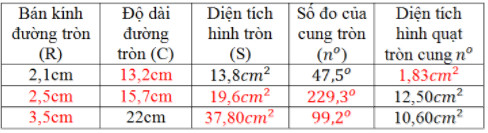
Điền vào các ô trống ta được các bảng sau:

Bài 83 trang 99 sgk Toán lớp 9 tập 2

Bài 83. a) Vẽ hình 62 (tạo bởi các cung tròn) với \(HI = 10cm\) và \(HO = 2cm\). Nêu cách vẽ.

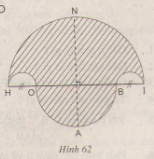
b) Tính diện tích hình \(HOABINH\) (miền gạch sọc)

c) Chứng tỏ rằng hình tròn đường kính \(NA\) có cùng diện tích với hình \(HOABINH\) đó.

Hướng dẫn giải:

a) Vẽ nửa đường tròn đường kính \(HI = 10 cm\), tâm \(M\)

Trên đường kính \(HI\) lấy điểm \(O\) và điểm \(B\) sao cho \(HO = BI = 2cm\).

Vẽ hai nửa đường tròn đường kính \(HO\), \(BI\) nằm cùng phía với đường tròn \((M)\).

vẽ nửa đường tròn đường kính \(OB\) nằm khác phía đối với đường tròn \((M)\). Đường thẳng vuông góc với \(HI\) tại \(M\) cắt \((M)\) tại \(N\) và cắt đường tròn đường kính \(OB\) tại \(A\).

b)  Diện tích hình \(HOABINH\) là:

\(\frac{1}{2}\).\(π.5^2\) + \(\frac{1}{2}\).\(π.3^2\) – \(π.1^2\) = \(\frac{25}{2}π\) + \(\frac{9}{2}π\) - \(π\) = \(16π\) (\(cm^2\)) (1)

c) Diện tích hình tròn đường kính \(NA\) bằng:

             \(π. 4^2 = 16π\)  (\(cm^2\))                                           (2)

So sánh (1) và (2) ta thấy hình tròn đường kính \(NA\) có cùng diện tích với hình \(HOABINH\)

Giaibaitap.me