Bài 15 trang 117 - Sách giáo khoa toán 9 tập 2
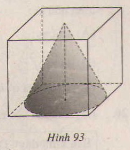
Bài 15 Một hình nón được đặt vào bên trong của một hình lập phương như hình vẽ (cạnh của hình lập phương bằng \(1\)). Hãy tính:
a) Bán kính đáy của hình nón.
b) Độ dài đường sinh.
Giải
a) Có đường tròn đáy của hình nón nội tiếp trong hình vuông của một mặt hình lập phương. Do đó bán kính của đáy hình nón bằng một nửa cạnh hình lập phương và bằng \(0,5\).
b) Đỉnh của hình nón tiếp xúc với một mặt của hình lập phương nên đường cao của hình nón bằng với cạnh của hình lập phương vàng bằng \(1\).
Theo định lí pytago, độ dài đường sinh của hình nón là :
\( l\) = \(\sqrt{1^2+ 0,5^2}\) = \(\frac{\sqrt{5}}{2}\).
Bài 16 trang 117 - Sách giáo khoa toán 9 tập 2
Bài 16. Cắt mặt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành \(1\) hình quạt. Biết bán kính của quạt bằng độ dài đường sinh và độ dài cũng bằng chu vi đáy.
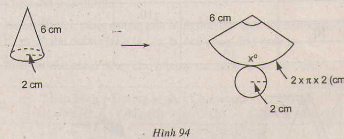
quan sát hình 94 và tính số đo cung của hình quạt.
Giải:
Độ dài \(l\) của cung hình quạt tròn bán kính \(6 cm\) bằng chu vi đáy của hình nón:
\(l = 2 π.2 = 4 π\)
Áp dụng công thức tính độ dài cung trong \(x^0\) ta có:
\(l\) = \(\frac{\pi Rx^o}{180}= 4\pi\)
Suy ra: \(x^0\) = \(\frac{4.180}{6}\) = \(120^0\).
Bài 17 trang 117 - Sách giáo khoa toán 9 tập 2
Bài 17. Khi quay tam giác vuông để tạo ra một hình nón như hinh 87 thì góc \(CAO\) gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là \(30^0\), độ dài đường sinh là \(a\). Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
Giải:
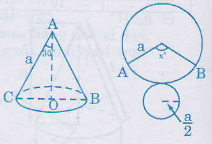
Theo đề bài: góc ở đỉnh cả hình nón là \(60^0\) nên suy ra đường kính của đường tròn đáy của một hình nón bằng \(a\)(do \(∆ABC\) đều). Vậy bán kính đáy của hình nón là \(\frac{a}{2}\)
Đường sinh của hình nón là \(a\).
Độ dài cung hình quạt trong \(n^0\), bán kính \(a\) bằng chu vi đáy hình tròn nên ta có:
\(\frac{\pi an^0}{2}= 2\pi\frac{a}{2}\)
Suy ra : \(n^0=180^0\)
Bài 18 trang 117 - Sách giáo khoa toán 9 tập 2
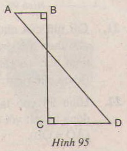
Bài 18. Hình \(ABCD\)(h95) khi quay quanh \(BC\) thì tạo ra:
(A) Một hình trụ;
(B) Một hình nón;
(C) Một hình nón cụt;
(D) Hai hình nón;
(E) Hai hình trụ.
Hãy chọn câu trả lời đúng.
Giải:
Gọi \(O\) là giao điểm của \(BC\) và \(AD\)
Khi quay hình \(ABCD\) quanh \(BC\) có nghĩa là tam giác vuông \(OBA\) quanh \(OB\) và tam giác vuông \(OCD\) quanh \(OC\). Mỗi hình quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ tạo ra \(2\) hình nón.
Vậy chọn D.
Giaibaitap.me
Giải bài tập trang 118 bài 2 hình nón - hình nón cụt, diện tích xung quanh và thể tích của hình nón, hình nón cụt SGK toán 9 tập 2. Câu 19: Hình khải triển của mặt xung quanh của một hình nón là một hình quạt...
Giải bài tập trang 119 bài 2 hình nón - hình nón cụt, diện tích xung quanh và thể tích của hình nón, hình nón cụt SGK toán 9 tập 2. Câu 23: Viết công thức tính nửa góc ở đỉnh của một hình nón...
Giải bài 27, 28, 29 bài 2 hình nón - hình nón cụt, diện tích xung quanh và thể tích của hình nón, hình nón cụt trang 119, 120 SGK toán 9 tập 2. Câu 27: Một phần dụng cụ gồm một phần có dạng trụ, phần còn lại có dạng nón...
Giải bài tập trang 124, 125 bài 3 hình cầu - diện tích hình cầu và thể tích hình cầu SGK toán 9 tập 2. Câu 30: Nếu thể tích của một hình cầu là...
