Bài 23 trang 119 - Sách giáo khoa toán 9 tập 2

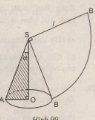
Bài 23 Viết công thức tính nửa góc ở đỉnh của một hình nón (góc \(a\) của tam giác vuông \(AOS\)- hình 99) sao cho diện tích khai triển mặt nón bằng một phần tư diện tích hình tròn (bán kính \(SA\)).

Giải:

Diện tích hình quạt : 

\(S_q = \frac{\pi r^2 n^o}{360^o}= \frac{\pi.l^2.90}{360}=\frac{\pi.l^2}4\)

Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\)

Theo đầu bài ta có: \({S_{xq}} = S_q \)=> \(πrl\)= \(\frac{\pi.l^2}4\)

Vậy \(l = 4r\) 

Suy ra \(sin(a) \)= \(\frac{r}l\) =\( 0,25\)

 Vậy \(a = {14^0}28'\)

Bài 24 trang 119 - Sách giáo khoa toán 9 tập 2

Bài 24. Hình khai triển mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là \(16cm\), số đo cung là \(120^0\) Tan của góc ở đỉnh hình nón là:

(A) \(\frac{\sqrt{2}}4\)               (B) \(\frac{\sqrt{2}}2\)          (C) \(\sqrt{2}\)            (D) 2\(\sqrt{2}\)

Giải

Đường sinh của hình nón là \(l = 16\). Độ dài cung \(AB\) của đường tròn chứa hình quạt là\(\frac{32. \pi}{3}\) , chu vi đáy bằng suy ra \(C= 2πr\) suy \(r\) = \(\frac{16}{3}\)

Trong tam giác vuông \(AOS\) có: \(h= \sqrt{16^2- (\frac{16}{3})^2}= 16\sqrt{\frac{8}{9}}= \frac{32}{3}\sqrt{2}\)

\(tan(a)\) = \(\frac{r}{h}\) = \(\frac{\sqrt{2}}{4}\)

Bài 25 trang 119 - Sách giáo khoa toán 9 tập 2

Bài 25. Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy \(a,b\) (\(a<b\)) và độ dài đường sinh là \(l\) (\(a,b,l\) có cùng đơn vị đo).

Giải:

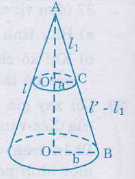
Kí hiệu như hình vẽ. Ta có hai tam giác vuông \(AO'C\) và \(AOB\) đồng dạng vì có góc chung.

 Nên \(\frac{l_1}{l - l_1}= \frac{a}b\) => \(l_1 = \frac{a}bl- \frac{a}bl_1\) 

=> \((1+\frac {a}b)l_1 = \frac{a}{b}l\) => \(l_1 = \frac{a}{a+b}l\)

Diện tích xung quanh của hình nón lớn: 

\(S\)_{xq nón lớn} = \(π.r.l =π.b.l\)

Diện tích xung quanh của hình nón nhỏ:

\(S\)_{xq nón nhỏ} =\(\pi .r.{l_1} = \pi .a.{a \over {a + b}}l = \pi {{{a^2}} \over {a + b}}l\)

Diện tích xung quanh của hình nón cụt là:

\(S\)_{xq nón cụt} =  \(S\)_{xq nón lớn} - \(S\)_{xq nón nhỏ}

= \(\pi b l - \pi \frac{a^2}{a +b}l=(b-\frac{a^2}{a+b})\pi l\)

= \((\frac{b^2+ab- a^2}{a+b})\pi l\)

Bài 26 trang 119 - Sách giáo khoa toán 9 tập 2

Bài 26 Hãy điền đầy đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm):

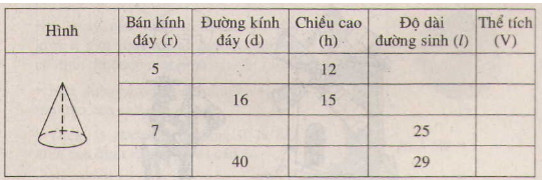
Giải:

Dòng thứ nhất: \(d = 2r =10\) 

\(l = \sqrt{h^2 + r^2}=\sqrt{12^2+5^2}= \sqrt{169}=13\)

\(V=\frac{1}{3} \pi r^2 h = \frac{1}{3} 3,14 . 5^2 . 12 = 314\)

Dòng thứ hai: \(r =  \frac{d}{2} = 8\)

\(l = \sqrt{h^2 + r^2}=\sqrt{15^2+8^2}= \sqrt{289}=17\)

\(V=\frac{1}{3} \pi r^2 h = \frac{1}{3} 3,14 . 8^2 . 15 = 1004,8\)

 Các dòng thứ ba, thứ tư ta làm tương tự

Ta được bảng sau:

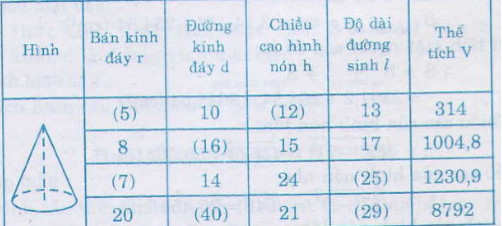
Giaibaitap.me