Bài 54 trang 63 SGK Toán 9 tập 2

Bài 54. Vẽ đồ thị của hàm số \(y = {1 \over 4}{x^2}\) và \(y =  - {1 \over 4}{x^2}\) trên cùng một hệ trục tọa độ

a) Qua điểm \(B(0; 4)\) kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số \(y = {1 \over 4}{x^2}\) tại hai điểm M và M’. Tìm hoành độ của M và M’.

b) Tìm trên đồ thị của hàm số \(y =  - {1 \over 4}{x^2}\) điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:

- Ước lượng trên hình vẽ:

- Tính toán theo công thức.

Giải:

Vẽ đồ thị hàm số:

* Hàm số \(y = {1 \over 4}{x^2}\) và \(y =  - {1 \over 4}{x^2}\)

- Tập xác định \(D = R\)

- Bảng giá trị

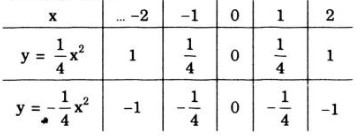
- Đồ thị hàm số \(y = {1 \over 4}{x^2}\) và \(y =  - {1 \over 4}{x^2}\) là các Parabol có đỉnh là gốc tọa độ O và nhận Oy làm trục đối xứng. Đồ thị hàm số \(y = {1 \over 4}{x^2}\) nằm trên trục hoành, đồ thị hàm số \(y =  - {1 \over 4}{x^2}\) nằm dưới trục hoành.

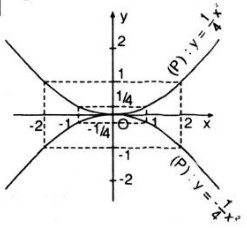
a) Đường thẳng qua \(B(0; 4)\) song song với \(Ox\) cắt đồ thị tại hai điểm \(M, M'\) (xem trên đồ thị). Từ đồ thị ta có hoành độ của \(M\) là \(x = 4\), của \(M'\) là \(x = - 4\).

b) Trên đồ thị hàm số \(y =  - {1 \over 4}{x^2}\) ta xác định được điểm \(N\) và \(N’\) có cùng hoành độ với \(M, M’\). ta được đường thẳng \(M, M’\)

Tìm tung độ của \(N, N’\)

- Ước lượng trên hình vẽ được tung độ của \(N\) là \(y = - 4\); của \(N’\) là \(y = -4\)

- Tính toán theo công thức:

Điểm \(N\) trên \(y =  - {1 \over 4}{x^2}\) có \(x = 4\) nên \(y =  - {1 \over 4}{.4^2} =  - 4\)

Điểm \(N’\) trên \(y =  - {1 \over 4}{x^2}\) có \(x = 4\) nên \(y =  - {1 \over 4}.{( - 4)^2} =  - 4\)

Vậy tung độ của \(N, N’ = -4\).

Bài 55 trang 63 SGK Toán 9 tập 2

Bài 55. Cho phương trình \(x^2 – x – 2 = 0\)

a) Giải phương trình

b) Vẽ hai đồ thị \(y = x^2\) và \(y = x + 2\) trên cùng một hệ trục tọa độ.

c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.

Hướng dẫn làm bài:

a) Giải phương trình: \(x^2 – x – 2 = 0\)

\(\Delta = (-1)^2– 4.1.(-2) = 1 + 8 > 0\)

\(\sqrt\Delta= \sqrt9 = 3\)

\(\Rightarrow {x_1} = -1; {x_2}= 2\)

b) Vẽ đồ thị hàm số

- Hàm số \(y = x^2\)

+ Bảng giá trị:

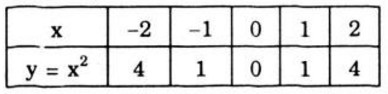
- Hàm số \(y = x + 2\)

+ Cho \(x = 0 ⇒ y = 2\) được điểm \(A(0;2)\)

+ Cho \(x = -2 ⇒ y = 0\) được điểm \(B(-2;0)\)

Đồ thị hàm số:

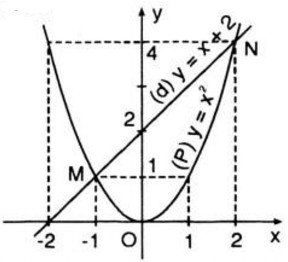
c) Ta có phương trình hoành độ giao điểm của hai đồ thị là:

\({x^2} = x + 2 \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow \left\{ \matrix{{x_1} = - 1 \hfill \cr {x_2} = 2 \hfill \cr} \right.\) 

Điều này chứng tỏ rằng đồ thị đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là \(x = -1; x= 2\). Hai giá trị này cũng chính là nghiệm của phương trình \(x^2 - x - 2 = 0\) ở câu a).

Bài 56 trang 63 SGK Toán 9 tập 2

Bài 56. Giải các phương trình:

a) \(3{{\rm{x}}^4} - 12{{\rm{x}}^2} + 9 = 0\)            

b) \(2{{\rm{x}}^4} + 3{{\rm{x}}^2} - 2 = 0\)

c) \({x^4} + 5{{\rm{x}}^2} + 1 = 0\)  

Hướng dẫn làm bài:

a) \(3{{\rm{x}}^4} - 12{{\rm{x}}^2} + 9 = 0\)   

Đặt \(t = {x^2}\left( {t \ge 0} \right)\) 

Ta có phương trình:

\(\eqalign{
& 3{t^2} - 12t + 9 = 0 \cr
& \Leftrightarrow {t^2} - 4t + 3 = 0 \cr} \) 

Phương trình có \(a + b + c = 0\) nên có hai nghiệm \({t_1} = 1; {t_2} = 3\) (đều thỏa mãn)

Với \({t_1} = 1 \Rightarrow {x^2} = 1 \Leftrightarrow x =  \pm 1\)

Với \({t_2} = 3 \Rightarrow {x^2} = 3 \Leftrightarrow x =  \pm \sqrt 3\)

b) \(2{{\rm{x}}^4} + 3{{\rm{x}}^2} - 2 = 0\)

Đặt \(t = {x^2}\left( {t \ge 0} \right)\)  

Ta có phương trình :

\(\eqalign{
& 2{t^2} + 3t - 2 = 0 \cr
& \Delta = 9 + 16 = 25 \Rightarrow \sqrt \Delta = 5 \cr
& \Rightarrow {t_1} = {{ - 3 + 5} \over 4} = {1 \over 2}(TM);{t_2} = - 2(loại) \cr}\)

Với \(t = {1 \over 2} \Rightarrow {x^2} = {1 \over 2} \Leftrightarrow x =  \pm \sqrt {{1 \over 2}}  =  \pm {{\sqrt 2 } \over 2}\)

c) \({x^4} + 5{{\rm{x}}^2} + 1 = 0\)    

Đặt \(t = {x^2}\left( {t \ge 0} \right)\) 

Ta có phương trình :

\(t^2 + 5t + 1 = 0\)

\(\Delta = 25 – 2 = 21\)

\(\eqalign{
& \Rightarrow {t_1} = {{ - 5 + \sqrt {21} } \over 2} < 0(loại) \cr
& {t_2} = {{ - 5 - \sqrt {21} } \over 2} < 0(loại) \cr} \) 

Vậy phương trình vô nghiệm

Bài 57 trang 63 SGK Toán 9 tập 2

Bài 57. Giải các phương trình:

a) \(5{{\rm{x}}^2} - 3{\rm{x}} + 1 = 2{\rm{x}} + 11\)                     

b) \({{{x^2}} \over 5} - {{2{\rm{x}}} \over 3} = {{x + 5} \over 6}\) 

c) \({x \over {x - 2}} = {{10 - 2{\rm{x}}} \over {{x^2} - 2{\rm{x}}}}\)                            

d) \({{x + 0,5} \over {3{\rm{x}} + 1}} = {{7{\rm{x}} + 2} \over {9{{\rm{x}}^2} - 1}}\) 

e) \(2\sqrt 3 {x^2} + x + 1 = \sqrt 3 \left( {x + 1} \right)\)              

f) \({x^2} + 2\sqrt 2 x + 4 = 3\left( {x + \sqrt 2 } \right)\)

Hướng dẫn làm bài:

a)

\(\eqalign{
& 5{{\rm{x}}^2} - 3{\rm{x}} + 1 = 2{\rm{x}} + 11 \cr
& \Leftrightarrow 5{{\rm{x}}^2} - 5{\rm{x}} - 10 = 0 \cr
& \Leftrightarrow {x^2} - x - 2 = 0 \cr}\)

Phương trình có \(a – b + c = 1 + 1 – 2 = 0\) nên có 2 nghiệm \({x_1}= -1; {x_2}= 2\)

b)

\(\eqalign{
& {{{x^2}} \over 5} - {{2{\rm{x}}} \over 3} = {{x + 5} \over 6} \cr
& \Leftrightarrow 6{{\rm{x}}^2} - 20{\rm{x}} = 5{\rm{x}} + 25 \cr
& \Leftrightarrow 6{{\rm{x}}^2} - 25{\rm{x}} - 25 = 0 \cr
& \Delta = {25^2} + 4.6.25 = 1225 \cr
& \sqrt \Delta = 35 \Rightarrow {x_1} = 5;{x_2} = - {5 \over 6} \cr} \)

c) \({x \over {x - 2}} = {{10 - 2{\rm{x}}} \over {{x^2} - 2{\rm{x}}}}\)  ĐKXĐ: \(x ≠ 0; x ≠ 2\)

\(\eqalign{
& \Leftrightarrow {x^2} = 10 - 2{\rm{x}} \cr
& \Leftrightarrow {x^2} + 2{\rm{x}} - 10 = 0 \cr
& \Delta ' = 1 + 10 = 11 \cr
& \Rightarrow {x_1} = - 1 + \sqrt {11} (TM) \cr
& {x_2} = - 1 - \sqrt {11} (TM) \cr} \)

d) \({{x + 0,5} \over {3{\rm{x}} + 1}} = {{7{\rm{x}} + 2} \over {9{{\rm{x}}^2} - 1}}\) ĐKXĐ: \(x \ne  \pm {1 \over 3}\)

\(\eqalign{
& \Leftrightarrow {{2{\rm{x}} + 1} \over {3{\rm{x}} + 1}} = {{14{\rm{x}} + 4} \over {9{{\rm{x}}^2} - 1}} \cr
& \Leftrightarrow \left( {2{\rm{x}} + 1} \right)\left( {3{\rm{x}} - 1} \right) = 14{\rm{x}} + 4 \cr
& \Leftrightarrow 6{{\rm{x}}^2} + x - 1 = 14{\rm{x}} + 4 \cr
& \Leftrightarrow 6{{\rm{x}}^2} - 13{\rm{x}} - 5 = 0 \cr
& \Delta = {( - 13)^2} - 4.6.( - 5) = 289 \cr
& \sqrt \Delta = \sqrt {289} = 17 \cr
& \Rightarrow {x_1} = {5 \over 2}(TM) \cr
& {x_2} = - {1 \over 3}(loại) \cr} \)

e)

\(\eqalign{
& 2\sqrt 3 {x^2} + x + 1 = \sqrt 3 \left( {x + 1} \right) \cr
& \Leftrightarrow 2\sqrt 3 {x^2} - \left( {\sqrt 3 - 1} \right)x + 1 - \sqrt 3 = 0 \cr
& \Delta = {\left( {\sqrt 3 - 1} \right)^2} - 8\sqrt 3 \left( {1 - \sqrt 3 } \right) \cr
& = 15 - 2.5.\sqrt 3 + 3 = {\left( {5 - \sqrt 3 } \right)^2} \cr
& \sqrt \Delta = \sqrt {{{\left( {5 - \sqrt 3 } \right)}^2}} = 5 - \sqrt 3 \cr
& \Rightarrow {x_1} = {{\sqrt 3 - 1 + 5 - \sqrt 3 } \over {4\sqrt 3 }} = {{\sqrt 3 } \over 3} \cr
& {x_2} = {{\sqrt 3 - 1 - 5 + \sqrt 3 } \over {4\sqrt 3 }} = {{1 - \sqrt 3 } \over 2} \cr}\) 

f)

\(\eqalign{
& {x^2} + 2\sqrt 2 x + 4 = 3\left( {x + \sqrt 2 } \right) \cr
& \Leftrightarrow {x^2} + \left( {2\sqrt 2 - 3} \right)x + 4 - 3\sqrt 2 = 0 \cr
& \Delta = 8 - 12\sqrt 2 + 9 - 16 + 12\sqrt 2 = 1 \cr
& \sqrt \Delta = 1 \cr
& \Rightarrow {x_1} = {{3 - 2\sqrt 2 + 1} \over 2} = 2 - \sqrt 2 \cr
& {x_2} = {{3 - 2\sqrt 2 - 1} \over 2} = 1 - \sqrt 2 \cr} \)

Giaibaitap.me