Bài 48 trang 59 sgk Toán 9 tập 2

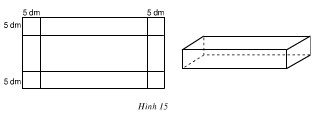
Bài 48. Từ một miếng tôn hình chữ nhật người ta cắt ở bốn góc bốn hình vuông có cạnh bằng \(5\) dm để làm thành một cái thùng hình hộp chữ nhật không nắp có dung tích \(1500\) dm³ (h.15). Hãy tính kích thước của miếng tôn lúc đầu, biết rằng chiều dài của nó gấp đôi chiều rộng.

Bài giải:

Gọi chiều rộng của miếng tôn là \(x\) (dm), \(x > 0\).

Chiều dài của nó là \(2x\) (dm)

Khi làm thành một cái thùng không đáy thì chiều dài của thùng là \(2x - 10\) (dm), chiều rộng là \(x - 10\) (dm), chiều cao là \(5\) (dm).

Dung tích của thùng là \(5(2x - 10)(x - 10)\) (dm³)

Theo đầu bài ta có phương trình:

\(5(2x - 10)(x - 10) = 1500\) hay

\(x^2 – 15x – 100 = 0\)

Giải phương trình: \(\Delta = 225 + 400 = 625\), \(\sqrt{\Delta} = 25\)

\({x_1} = 20, {x_2} = -5\) (loại)

Vậy miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40 (dm).

Bài 49 trang 59 sgk Toán 9 tập 2

Bài 49. Hai đội thợ quét sơn một ngôi nhà. Nếu họ cùng làm thì trong 4 ngày xong việc. Nếu họ làm riêng thì đội I hoàn thành công việc nhanh hơn đội II là 6 ngày. Hỏi nếu làm riêng thì mỗi đội phải làm trong bao nhiêu ngày để xong việc ?

Bài giải:

Gọi thời gian đội I làm một mình xong việc là \(x\) (ngày), \(x > 0\).

Vì đội II hoàn thành công việc lâu hơn đội I là 6 ngày nên thời gian một mình đội II làm xong việc là \(x + 6\) (ngày).

Mỗi ngày đội I làm được \(\frac{1}{x}\) (công việc).

Mỗi ngày đội II làm được \(\frac{1}{x+6}\) (công việc)

Hai đội làm 4 ngày xong công việc nên mỗi ngày cả hai đội làm được \(\frac{1}{4}\) công việc ta có phương trình:

\(\frac{1}{x}\) + \(\frac{1}{x+6}\) = \(\frac{1}{4}\)

Giải phương trình: \(x(x + 6) = 4x + 4x + 24\) hay \(x^2– 2x - 24 = 0\), \(\Delta' = 1 + 24 = 25 = 5^2\)

\({x_1} = 1 + 5 = 6, {x_2} = 1 - 5 = -4\)

Vì \(x > 0\) nên \({x_2} = 1 - 5 = -4\) không thỏa mãn điều kiện của ẩn.

Vậy một mình đội I làm trong \(6\) ngày thì xong việc.

Một mình đội II làm trong \(12\) ngày thì xong việc.

Bài 50 trang 59 sgk Toán 9 tập 2

Bài 50. Miếng kim loại thứ nhất nặng \(880\) g, miếng kim loại thứ hai nặng \(858\) g. Thể tích của miếng thứ nhất nhỏ hơn thể tích của miếng thứ hai là \(10\) cm³, nhưng khối lượng riêng của miếng thứ nhất lớn hơn khối lượng riêng của miếng thứ hai là \(1\) g/cm³ . Tìm khối lượng riêng của mỗi miếng kim loại.

Bài giải:

Gọi khối lượng riêng của miếng kim loại thứ nhất là: \(x\) (g/cm³ )

Khối lượng riêng của miếng kim loại thứ hai là: \(x - 1\) (g/cm³ )

Thể tích của miếng kim loại thứ nhất là: \(\frac{880}{x}\)  (cm³ )

Thể tích của miếng kim loại thứ hai là: \(\frac{858}{x-1}\) (cm³ )

Theo đầu bài thể tích của miếng thứ nhất nhỏ hơn miếng thứ hai là \(10\) cm³ nên ta có phương trình: \(\frac{858}{x-1} - \frac{880}{x} = 10\)

Giải phương trình:

\(10x(x - 1) = 858x - 880x + 880\) hay \(5x^2 + 6x - 440 = 0\)

\(\Delta'=9 + 2200 = 2209\), \(\sqrt{\Delta' }= 47\)

\({x_1}= 8,8, {x_2} = -10\)

Vì \(x > 0\) nên \({x_2} = -10\) (loại)

Vậy khối lượng riêng của miếng kim loại thứ nhất là: \(8,8\) g/cm³

Khối lượng riêng của miếng kim loại thứ hai là: \(7,8\) g/cm³

Giaibaitap.me