Bài 36 trang 82 sgk Toán lớp 9 tập 2

Bài 36. Cho đường tròn $(O)$ và hai dây $AB$, $AC$. Gọi $M, N$ lần lượt là điểm chính giữa của cung $AB$ và cung $AC$. Đường thẳng $MN$ cắt dây $AB$ tại $E$ và cắt dây $AC$ tại $H$. Chứng minh rằng tam giác $AEH$ là tam giác cân.

Hướng dẫn giải:

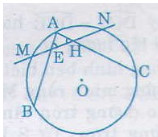
Ta có: $\widehat {AHM}$= $\frac{sđ\overparen{AM}+sđ\overparen{NC}}{2}$     (1)

           $\widehat {AEN}$= $\frac{sđ\overparen{MB}+sđ\overparen{AN}}{2}$           (2)

(Vì  \widehat {AHM}\)và  $\widehat {AEN}$là các góc có đỉnh cố định ở bên trong đường tròn).

Theo gỉả thiết thì:

$\overparen{AM}=\overparen{MB}   (3)$

$\overparen{NC}=\overparen{AN}    (4)$

Từ (1),(2), (3), (4), suy ra $\widehat {AHM}$= $\widehat {AEN}$ do đó $∆AEH$ là tam giác cân.

Bài 37 trang 82 sgk Toán lớp 9 tập 2

Bài 37. Cho đường tròn $(O)$ và hai dây $AB$, $AC$ bằng nhau. Trên cung nhỏ $AC$ lấy một điểm $M$. Gọi $S$ là giao điểm của $AM$ và $BC$. Chứng minh: $\widehat {ASC}$=$\widehat {MCA}$

Hướng dẫn giải:

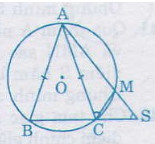
Ta có: $\widehat {ASC}$= $\frac{sđ\overparen{AB}+sđ\overparen{MC}}{2}$  (1)

($\widehat {ASC}$ là góc có đỉnh nằm bên ngoài đường tròn $(O)$)

và $\widehat {MCA}$=$\frac{sđ\overparen{AM}}{2}$   (2)

(góc nội tiếp chắn cung $\overparen{AM}$)

Theo giả thiết thì:

     $AB = AC =>$$\overparen{AB}=\overparen{AC}$   (3)

Từ (1), (2), (3) suy ra: $\overparen{AB}-\overparen{MC}=\overparen{AC}-\overparen{MC}=\overparen{AM}$

Từ đó $\widehat {ASC}=\widehat {MCA}$.

Bài 38 trang 82 sgk Toán lớp 9 tập 2

Bài 38. Trên một đường tròn, lấy liên tiếp ba cung $AC, CD, DB$ sao cho

$sđ\overparen{AC}$=$sđ\overparen{CD}$=$sđ\overparen{DB}$=$60^0$. Hai đường thẳng $AC$ và $BD$ cắt nhau tại $E$. Hai tiếp tuyến của đường tròn tại $B$ và $C$ cắt nhau tại $T$. Chứng minh rằng:

a) $\widehat {AEB}=\widehat {BTC}$;

b) $CD$ là phân giác của $\widehat{BTC}$

Hướng dẫn giải:

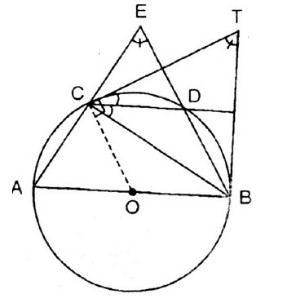
a) Ta có $\widehat{AEB}$ là góc có đỉnh ở bên ngoài đường tròn nên:

$\widehat{AEB}$=$\frac{sđ\overparen{AB}-sđ\overparen{CD}}{2}$=${{{{180}^0} - {{60}^0}} \over 2} = {60^0}$

và $\widehat{BTC}$  cũng là góc có đỉnh ở bên ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:

$\widehat{BTC}$=$\frac{\widehat {BAC}-\widehat {BDC}}{2}$=${{({{180}^0} + {{60}^0}) - ({{60}^0} + {{60}^0})} \over 2} = {60^0}$

  Vậy $\widehat {AEB} =\widehat {BTC}$ 

b)  $\widehat {DCT}$ là góc tạo bởi tiếp tuyến và dây cung nên:

         $\widehat {DCT}=\frac{sđ\overparen{CD}}{2}$

$\widehat {DCB}$ là góc nội tiếp trên 

          $\widehat {DCB}=\frac{sđ\overparen{DB}}{2}={{{{60}^0}} \over 2} = {30^0}$

Vậy  $\widehat {DCT}=\widehat {DCB}$  hay  $CD$ là phân giác của $\widehat {BCT}$

Bài 39 trang 83 sgk Toán lớp 9 tập 2

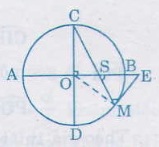
Bài 39. Cho $AB$ và $CD$ là hai đường kính vuông góc của đường tròn $(O)$. Trên cung nhỏ $BD$ lấy một điểm $M$. Tiếp tuyến tại $M$ cắt tia $AB$ ở $E$, đoạn thẳng $CM$ cắt $AB$ ở $S$.Chứng minh $ES = EM$.

Hướng dẫn giải:

Ta có $\widehat{MSE}$ = $\frac{sđ\overparen{CA}+sđ\overparen{BM}}{2}$ (1)

( vì $\widehat{MSE}$ là góc có đỉnh S ở trong đường tròn (O))

$\widehat{CME}$ = $\frac{sđ\overparen{CM}}{2}$= $\frac{sđ\overparen{CB}+sđ\overparen{BM}}{2}$ (2)

($\widehat{CME}$ là góc tạo bởi tiếp tuyến và dây cung).

Theo giả thiết         $\overparen{CA}=\overparen{CB}$           (3)

Từ (1), (2), (3) ta có: $\widehat{MSE}$ = $\widehat{CME}$ từ đó $∆ESM$ là tam giác cân và $ES = EM$

Giaibaitap.me