Bài 50 trang 87 sgk Toán lớp 9 tập 2

Bài 50. Cho đường tròn đường kính $AB$ cố định. $M$ là một điểm chạy trên đường tròn. Trên tia đối của tia $MA$ lấy điểm $I$ sao cho $MI = 2MB$.

a) Chứng minh $\widehat{AIB}$ không đổi.

b) Tìm tập hợp các điểm $I$ nói trên.

Hướng dẫn giải:

a) Vì $\widehat{BMA}$ = $90^0$  (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông $MIB$ có $tg\widehat{AIB}$ = $\frac{MB}{MI}$ = $\frac{1}{2}$ =>$\widehat{AIB}$ = $26^0 34'$ 

Vậy $\widehat{AIB}$ không đổi.

b) Phần thuận:

Khi điểm $M$ chuyển động trên đường tròn đường kính $AB$ thì điểm $I$ cũng chuyển động, nhưng luôn nhìn đoạn thẳng $AB$ cố định dưới góc $26^0 34'$ , vậy điểm $I$ thuộc hai cung chứa góc $26^0 34'$ dựng trên đoạn thẳng $AB$ (hai cung $\overparen{AmB}$ và $\overparen{Am'B}$)

Phần đảo:

Lấy điểm $I'$ bất kì thuộc $\overparen{AmB}$

hoặc $\overparen{Am'B}$, $I'A$ cắt đường tròn đường kính $AB$ tại $M'$.

Tam giác vuông $BMT$, có $tg\widehat{I'}$ = $\frac{M'B}{M'I'}$ = $tg26^034’$

Kết luận: Quỹ tích điểm $I$ là hai cung $\overparen{AmB}$ và $\overparen{Am'B}$

Bài 51 trang 87 sgk Toán lớp 9 tập 2

Bài 51. Cho $I, O$ lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác $ABC$ với $\widehat{A}$ = $60^0$. Gọi $H$ là giao điểm của các đường cao $BB'$ và $CC'$

Chứng minh các điểm $B, C, O, H, I$ cùng thuộc một đường tròn.

Hướng dẫn giải:

Ta có: $\widehat{BOC}$ = $2\widehat{BAC}$ =  $2.60^0$ = $120^0$       (1)

(góc nội tiếp và góc ở tâm cùng chắn một cung)

và $\widehat{BHC}$ = $\widehat{B'HC'}$ (đối đỉnh)

mà $\widehat{B'HC'}$ = $180^0$ - $\widehat{A}$ = $180^0- 60^0 = 120^0$

nên $\widehat{BHC}$ = $120^0$                 ⁽²⁾

$\widehat{BIC}$ = $\widehat{A}$ + $\frac{\widehat{B}+\widehat{C}}{2}$

          = $60^0$ + $\frac{180^{\circ}-60^{\circ}}{2}$ = $60^0+ 60^0$ 

(sử dụng góc ngoài của tam giác)

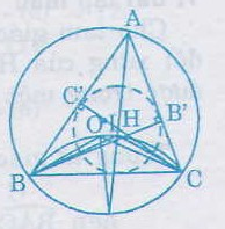
Do đó $\widehat{BIC}$ = $120^0$

Từ (1), (2), (3) ta thấy các điểm $O, H, I$ cùng nằm trên các cung chứa góc $120^0$ dựng trên đoạn thẳng $BC$. Nói cách khác, năm điểm $B, C, O, H, I$ cùng thuộc một đường tròn

Bài 52 trang 87 sgk Toán lớp 9 tập 2

Bài 52. "Góc sút" của quả phạt đền $11$ mét là bao nhiêu độ? Biết rằng chiều rộng cầu môn là $7,32m$. Hãy chỉ ra hai vị trí khác trên sân có cùng "góc sút" như quả phạt đền $11 m$.

Hướng dẫn giải:

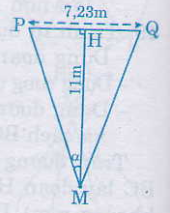
Gọi vị trí đặt bóng để sút phạt đền là $M$, và bề ngang cầu môn là $PQ$ thì $M$ nằm trên đường trung trực của $PQ$. Gọi $H$ là trung điểm $PQ$, $\widehat{PMH}$ = $\alpha$.

Theo các giả thiết đã cho thì trong tam giác vuông $MHP$, ta có:

$tgα$ = $\frac{3,66}{11}$ $≈ 0,333 => α = 18^036’$.

Vậy góc sút phạt đền là $2α ≈ 37^012’$.

Giaibaitap.me