Bài 47 trang 86 sgk Toán lớp 9 tập 2
Bài 47. Gọi cung chứa góc \(55^0\) ở bài tập 46 là \(\overparen{AmB}\). Lấy điểm \({M_1}\) nằm bên trong và điểm \({M_2}\) nằm bên ngoài đường tròn chứa cung này sao cho \({M_1},{M_2}\) và cung \(\overparen{AmB}\) nằm cùng về một phía đối với đường thẳng \(AB\). Chứng minh rằng:
a) \(\widehat {A{M_1}B} > 55^0\);
b) \(\widehat {A{M_2}B} < 55^0\).
Hướng dẫn giải:
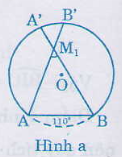
\({M_1}\) là điểm bất kì nằm trong cung chứa góc \(55^0\) (hình a).
Gọi \(B’, A’\) theo thứ tự là giao điểm của \({M_1}A\), \({M_1}B\) với cung tròn. Vì \(\widehat{A{M_1}B}\) là góc có đỉnh nằm trong đường tròn, nên: \(\widehat {A{M_1}B}\) = \(\frac{sđ\overparen{AB}+sđ\overparen{A'B'}}{2}\) = \(55^0\)+ (một số dương).
Vậy \(\widehat {A{M_1}B} > 55^0\)
b)
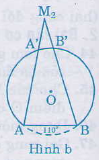
\({M_2}\) là điểm bất kì nằm ngoài đường tròn (h.b), \({M_2}A,{M_2}B\) lần lượt cắt đường tròn tại \(A’, B’.\) Vì góc \(\widehat {A{M_2}B}\) là góc có đỉnh nằm bên ngoài đường tròn nên:
\(\widehat {A{M_2}B}\)=\(\frac{sđ\overparen{AB}-sđ\overparen{A'B'}}{2}\)=\(55^0\)- (một số dương)
Vậy \(\widehat {A{M_2}B} < 55^0\)
Bài 48 trang 87 sgk Toán lớp 9 tập 2
Bài 48. Cho hai điểm \(A, B\) cố định. Từ \(A\) vẽ các tiếp tuyến với đường tròn tâm \(B\) bán kính không lớn hơn \(AB\). Tìm quỹ tích các tiếp điểm.
Hướng dẫn giải:
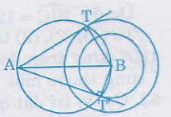
- Trường hợp các đường tròn tâm \(B\) có bán kính \(BA\). Tiếp tuyến \(BA\) vuông góc với bán kính \(BT\) tại tiếp điểm \(T\).
Do \(AB\) cố định nên quỹ tích của \(T\) là đường tròn đường kính \(AB\).
- Trường hợp các đường tròn tâm \(B\) có bán kính lớn hơn \(BA\): quỹ tích là tập hợp rỗng.
Bài 49 trang 87 sgk Toán lớp 9 tập 2
Bài 49. Dựng tam giác \(ABC\), biết \(BC = 6cm\), \(\widehat{A}\) = \(40^0\) và đường cao \(AH = 4cm\).
Hướng dẫn giải:
Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng \(BC = 6cm\)
- Dựng cung chứa góc \({40^0}\) trên đoạn thẳng \(BC\).
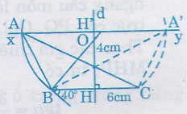
- Dựng đường thẳng \(xy\) song song với \(BC\) và cách \(BC\) một khoảng là \(4cm\) như sau:
Trên đường trung trực \(d\) của đoạn thẳng \(BC\) lấy đoạn \(HH' = 4cm\) (dùng thước có chia khoảng mm). Dựng đường thẳng \(xy\) vuông góc với \(HH'\) tại \(H\).
Gọi giao điểm \(xy\) và cung chứa góc là \(\widehat{A}\), \(\widehat{A'}\). Khi đó tam giác \(ABC\) hoặc \(A'BC\) đều thỏa yêu cầu của đề toán
Giaibaitap.me
Giải bài tập trang 87 bài 6 cung chứa góc SGK Toán lớp 9 tập 2. Câu 50: Cho đường tròn đường kính...
Giải bài tập trang 89 bài 7 tứ giác nội tiếp SGK Toán lớp 9 tập 2. Câu 53: Hãy điền vào ô trống trong bẳng sau (nếu có thể)...
Giải bài tập trang 89, 90 bài 7 tứ giác nội tiếp SGK Toán lớp 9 tập 2. Câu 57: Trong các hình sau, hình nào nội tiếp được một đường tròn...
Giải bài tập trang 91, 92 bài 8 đường tròn ngoại tiếp, đường tròn nội tiếp SGK Toán lớp 9 tập 2. Câu 61: Vẽ hình vuông nội tiếp đường tròn ...
