Bài 33 trang 80 sgk Toán lớp 9 tập 2
Bài 33. Cho \(A, B, C\) là ba điểm của một đường tròn. \(At\) là tiếp tuyến của đường tròn tại \(A\). Đường thẳng song song với \(At\) cắt \(Ab\) tại \(M\) và cắt \(AC\) tại \(N\).
Chứng minh: \(AB. AM = AC . AN\)
Hướng dẫn giải:
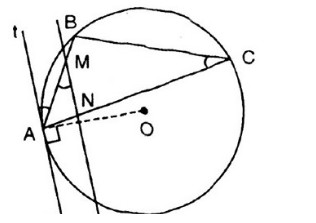
Ta có \(\widehat M = \widehat {BAt}\) (so le trong) (1)
\(\widehat {BAt} = \widehat C\) (2)
(góc tạo bởi tiếp tuyến và dây cung, chắn cung \(AB\), \(\widehat C\) là góc nội tiếp chắn cung \(AB\))
Từ (1) và (2) suy ra:
\(\widehat M = \widehat C\) (3)
Xét hai tam giác \(AMN\) và \(ACB\). chúng có:
\(\widehat A\) chung
\(\widehat M = \widehat C\)
Vậy \(∆AMN\) đồng dạng \(∆ACB\), từ đó \({{AN} \over {AB}} = {{AM} \over {AC}}\),
suy ra \(AB. AM = AC . AN\)
Bài 34 trang 80 sgk Toán lớp 9 tập 2
Bài 34. Cho đường tròn \((O)\) và điểm \(M\) nằm bên ngoài đường tròn đó. Qua điểm \(M\) kẻ tiếp tuyến \(MT\) và cát tuyến \(MAB\)
Chứng minh \(MT^2 = MA. MB\).
Hướng dẫn giải:
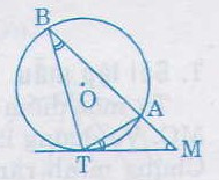
Xét hai tam giác \(BMT\) và \(TMA\), chúng có:
\(\widehat{M}\) chung
\(\widehat{B}\) = \(\widehat{T}\) (cùng chắn cung nhỏ \(\overparen{AT}\))
nên \(∆BMT\) đồng dạng \(∆TMA\), suy ra \(\frac{MT}{MA}\) = \(\frac{MB}{MT}\)
hay \(MT^2 = MA. MB\)
Bài 35 trang 80 sgk Toán lớp 9 tập 2
Bài 35. Trên bờ biển có ngọn hải đăng cao \(40m\). Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn đèn này biết rằng mắt người quan sát ở độ cao \(10 m\) so với mực nước biển và kính Trái Đất gần bằng \(6 400 km\) (h.30)?
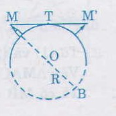
Hướng dẫn giải:
Áp dụng kết quả bài tập 34 ta có:
\(MT^2 = MA. MB\)
\(MT^2 = MA.(MA + 2R)\)
Thay số vào đẳng thức trên và lấy đơn vị là km, ta có:
\(MT^2 = 0,04 (0,04 + 12.800)\)
\(MT ≈ 23 (km)\)
Cũng tương ta có;
\(MT^2 = 0,01(0,01 +12.800)\)
\(MT ≈ 11 (km)\)
Từ đó: \(MM' = MT + M'T = 23+11= 34(km)\)
Vậy khi ngọn hải đăng khoảng \(34 km\) thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.
Giaibaitap.me
Giải bài tập trang 82, 83 bài 5 góc có đỉnh ở bên trong đường tròn, góc có đỉnh ở bên ngoài đường tròn SGK Toán lớp 9 tập 2. Câu 36: Chứng minh rằng...
Giải bài tập trang 83 bài 5 góc có đỉnh ở bên trong đường tròn, góc có đỉnh ở bên ngoài đường tròn SGK Toán lớp 9 tập 2. Câu 40: Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn...
Giải bài tập trang 86 bài 6 cung chứa góc SGK Toán lớp 9 tập 2. Câu 44: Cho tam giác...
Giải bài tập trang 86, 87 bài 6 cung chứa góc SGK Toán lớp 9 tập 2. Câu 47: Chứng minh rằng...
