Bài 23 trang 76 sgk Toán lớp 9 tập 2

Bài 23. Cho đường tròn \((O)\) và một điểm \(M\) cố định không nằm trên đường tròn. Qua \(M\) kẻ hai đường thẳng. Đường thẳng thứ nhất cắt \((O)\) tại \(A\) và \(B\).Đường thẳng thứ nhất cắt \((O)\) tại \(C\) và \(D\).

Chứng minh \(MA. MB = MC. MD\)

Hướng dẫn giải:

Xét hai trường hợp:

a) \(M\) ở bên trong đường tròn (hình a)

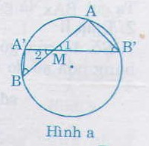
Xét hai tam giác \(MAB'\) và \(MA'B\) có:

              \(\widehat{M_{1}}\) = \(\widehat{M_{2}}\) ( đối đỉnh)

              \(\widehat{B'}\) = \(\widehat{B}\) (hai góc nội tiếp cùng chắn cung  \(AA'\)).

Do đó \(∆MAB'\) đồng dạng \(∆MA'B\), suy ra:

             \(\frac{MA}{MA'}\) = \(\frac{MB'}{MB}\), do đó \(MA. MB = MB'. MA'\)

b) \(M ở bên ngoài đường tròn (hình b)

Tương tự ta có:

\(∆MAB'\) đồng dạng \(∆MA'B\)

     \(\widehat{M}\) chung  

     \(\widehat{B'}\) = \(\widehat{B}\) (hai góc nội tiếp cùng chắn cung \(AA'\)).

Suy ra:     \(\frac{MA}{MA'}\) = \(\frac{MB'}{MB}\)

          hay \(MA. MB = MB'. MA'\)

Bài 24 trang 76 sgk Toán lớp 9 tập 2

Bài 24. Một chiếc cầu được thiết kế như hình 21 có độ dài \(AB = 40\)m, chiều cao \(MK = 3\)m. Hãy tính bán kính của đường tròn chứa cung \(AMB\)

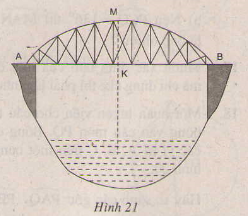
Hướng dẫn giải:

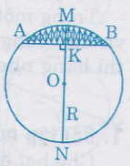
Gọi \(MN = 2R\) là đường kính của đường tròn có cung tròn là \(AMB\) 

Theo bài tập 23, ta có: 

             \(KA. KB = KM. KN\)

      hay \(KA. KB = KM. (2R - KM)\)

Thay số, ta có:

              \(20. 20 = 3(2R - 3)\)

     do đó \(6R = 400 + 9 = 409\).

Vậy \(R\) = \(\frac{409}{6}\) \(≈68,2\) (mét)

Bài 25 trang 76 sgk Toán lớp 9 tập 2

Bài 25. Dựng một tam giác vuông, biết cạnh huyền dài \(4\)cm và một cạnh góc vuông dài \(2,5\) cm.

Hướng dẫn giải:

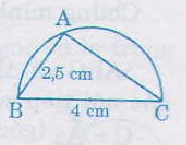
Cách vẽ như sau:

- Vẽ đoạn thẳng \(BC\) dài \(4cm\).

- Vẽ nửa đưởng tròn đường kính \(BC\).

- Vẽ dây \(AB\) (hoặc dây \(CA\)) dài \(2,5cm\).

Ta có tam giác thỏa mãn các yêu cầu của đầu bài ( \(\widehat{A}\)=\(90^{\circ}\), \(BC = 4cm, AB = 2,5cm\))

Bài 26 trang 76 sgk Toán lớp 9 tập 2

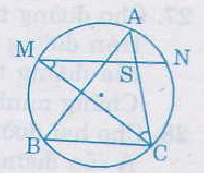
Bài 26. Cho \(AB, BC, CA \) là ba dây của đường tròn \((O)\). Từ điểm chính giữa \(M\) của \(\overparen{AB}\) vẽ dây \(MN\) song song với dây \(BC\). Gọi giao điểm của \(MN\) và \(AC\) là \(S\). Chứng minh \(SM = SC\) và \(SN = SA\)

Hướng dẫn giải:

Ta có:

\(\overparen{MA}\)= \(\overparen{MB}\) (theo gt).

\(\overparen{NC}\)= \(\overparen{MB}\) ( vì \(MN // BC\))

Suy ra \(\overparen{MA}\) = \(\overparen{NC}\), do đó \(\widehat {ACM} = \widehat {CMN}\)

Vậy \(∆SMC\) là tam giác cân, suy ra \(SM = SC\)

Chứng minh tương tự ta cũng có \(∆SAN\) cân , \(SN = SA\).

Giaibaitap.me