Bài 12 trang 106 sgk Toán 9 - tập 1
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8 cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI=1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD=AB.
Hướng dẫn giải:
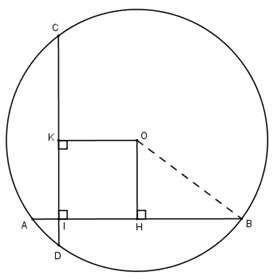
a) Vẽ \(OH\perp AB\), ta có
\(HA=HB=4cm.\)
Xét tam giác HOB vuông tại H, có:
\(OH^{2}=OB^{2}-HB^{2}=5^{2}-4^{2}=9\Rightarrow OH=3(cm)\).
b) Vẽ \(OK\perp CD\).
Tứ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra \(OK=HI\). Ta có \(HI=4-1=3cm\), suy ra \(OK=3cm.\)
Vậy \(OH=OK = 3cm.\)
Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó \(AB = CD.\)
Bài 13 trang 106 sgk Toán 9 - tập 1
Bài 13. Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:
a) EH = EK
b) EA = EC.
Hướng dẫn giải:
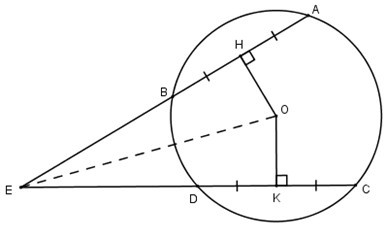
a) Vì \(HA=HB\) nên \(OH\perp AB\).
Vì \(KC=KD\) nên \(OK\perp CD\).
Mặt khác, \(AB=CD\) nên \(OH=OK\) (hai dây bằng nhau thì cách đều tâm).
\(\Delta HOE=\Delta KOE\) (cạnh huyền, cạnh góc vuông)
Suy ra \(EH=EK. (1)\)
b) Ta có \(AH=KC\) (một nửa của hai dây bằng nhau). (2)
Từ (1) và (2) suy ra \(EH+HA=EK+KC\)
hay \(EA=EC.\)
Bài 14 trang 106 sgk Toán 9 - tập 1
Bài 14. Cho đường tròn tâm \(O\) bán kính \(25cm\), dây \(AB\) bằng \(40cm\). Vẽ dây \(CD\) song song với \(AB\) và có khoảng cách đến \(AB\) bằng \(22cm\). Tính độ dài dây \(CD\).
Giải
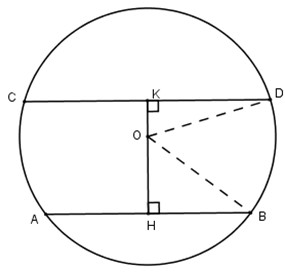
Vẽ \(OH\perp AB\), đường thẳng \(OH\) cắt \(CD\) tại \(K\).
Ta có
\(OK\perp CD\)
\(KC=KD\)
\(AH=HB\)
Áp dụng định lí Pytago vào tam giác \(OBH\) vuông tại \(H\), ta có:
\(OH=\sqrt{OB^2-\left ( \frac{AB}{2} \right )^2}=15(cm)\)
\(\Rightarrow OK=22-15=7(cm)\)
Áp dụng định lí Pytago vào tam giác \(OKD\) vuông tại \(K\), ta có:
\(KD=\sqrt{OD^2-OK^2}=24(cm)\)
\(\Rightarrow CD=2KD=48(cm)\)
Giaibaitap.me
Giải bài tập trang 106 bài 3 liên hệ giữa dây và khoảng cách từ tâm đến dây SGK Toán 9 tập 1. Câu 15: Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết...
Giải bài tập trang 109 bài 4 vị trí tương đối của đường thẳng và đường tròn SGK Toán 9 tập 1. Câu 17: Điền vào các chỗ trống (...) trong bảng sau...
Giải bài tập trang 111 bài 5 dấu hiệu nhận biết tiếp tuyến của đường tròn SGK Toán 9 tập 1. Câu 21: Cho tam giác ABC có AB=3, AC=4, BC=5. Vẽ đường tròn (B;BA)...
Giải bài tập trang 111 bài 5 dấu hiệu nhận biết tiếp tuyến của đường tròn SGK Toán 9 tập 1. Câu 24: Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C...
