Bài 24 trang 111 sgk Toán 9 - tập 1
Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C.
a) Chứng minh rằng CB là tiếp tuyến của đường tòn.
b) Cho bán kính của đường tròn bằng 15cm, AB=24cm. Tính độ dài OC.
Giải:
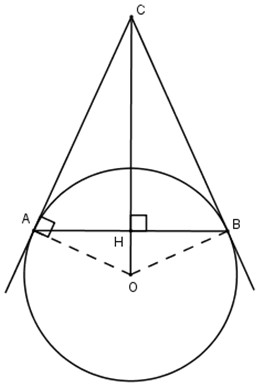
a) Gọi H là giao điểm của OC và AB.
Vì \(OH\perp AB\) nên \(HA=HB\), suy ra OC là đường trung trực của AB, do đó \(CB=CA.\)
\(\Delta CBO=\Delta CAO\) (c.c.c)
\(\Rightarrow \widehat{CBO}=\widehat{CAO}\).
Vì AC là tiếp tuyến của đường trong (O) nên:
\(AC\perp OA\Rightarrow \widehat{CAO}=90^{\circ}\).
Do đó \(\widehat{CBO}=90^{\circ}\).
Vậy CB là tiếp tuyến của đường tròn (O).
b) Xét tam giác HOA vuông tại H, có
\(OH^{2}=OA^{2}-AH^{2}\)
\(=15^{2}-12^{2}=81\)
\(\Rightarrow OH=9(cm)\)
Xét tam giác BOC vuông tại B, có:
\(OB^{2}=OC\cdot OH\)
\(\Rightarrow OC=\frac{OB^{2}}{OH}=\frac{225}{9}=25(cm).\)
Nhận xét. Ở câu a) ta đã dùng dấu hiệu nhận biết tiếp tuyến để chứng minh CB là tiếp tuyến của đường tròn (O). Ta cũng có thể dựa vào tính chất đối xứng của đường kính để chứng minh CB là tiếp tuyến. Thực vậy B và A đối xứng qua đường thẳng chứa đường kính CO, mà CA là tiếp tuyến nên CB phải là tiếp tuyến.
Bài 25 trang 111 sgk Toán 9 - tập 1
Cho đường tròn tâm O có bán kính OA=R, dây BC vuông góc với OA tại trung điểm M của OA.
a) Từ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.
Hướng dẫn giải:
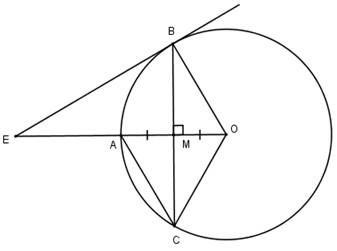
a) Ta có \(OA\perp BC\Rightarrow MB=MC\).
Mặt khác:
\(MA=MO\) nên tứ giác ABOC là hình bình hành.
Hình bình hành này có hai đường chéo vuông góc nên là hình thoi.
b) Ta có \(BA=BO\) (hai cạnh hình thoi) mà \(BO=OA\) (bán kính) nên tam giác ABO là tam giác đều.
Suy ra \(\widehat{BOA}=60^{\circ}\).
Ta có EB là tiếp tuyến \(\Rightarrow EB\perp OB\).
Xét tam giác BOE vuông tại B, có:
\(BE=BO\cdot tg60^{\circ}= R.tg60^0=R\sqrt{3}.\)
Giaibaitap.me
Giải bài tập trang 115, 116 bài 6 tính chất của hai tiếp tuyến cắt nhau SGK Toán 9 tập 1. Câu 26: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm)...
Giải bài tập trang 116 bài 6 tính chất của hai tiếp tuyến cắt nhau SGK Toán 9 tập 1. Câu 30: Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn)...
Giải bài tập trang 119, 123 bài 7 + 8 vị trí tương đối của hai đường tròn SGK Toán 9 tập 1. Câu 33: Trên hình 89 hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC//O'D...
Giải bài tập trang 122, 123 bài 7 + 8 vị trí tương đối của hai đường tròn SGK Toán 9 tập 1. Câu 35: Điền vào các ô trống trong bảng, biết rằng hai đường tròn (O;R) và (O';r) có...
