Câu 9 trang 50 SGK Đại số 10

Xét chiều biến thiên và vẽ đồ thị của các hàm số

a) \(y = {1 \over 2}x - 1\)

b) \(y = 4 - 2x\)

c) \(y = \sqrt {{x^2}} \)

d) \(y = |x+1|\)

Giải

a) \(y = {1 \over 2}x - 1\)

Bảng biến thiên

Đồ thị hàm số

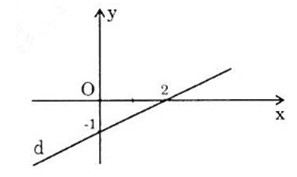
Đồ thị là đường thẳng đi qua \(2\) điểm:

+ Giao với trục tung \(P(0,-1)\)

+ Giao với trục hoành \(Q(2, 0)\)

b) \(y = 4 - 2x\)

Bảng biến thiên

Đồ thị hàm số

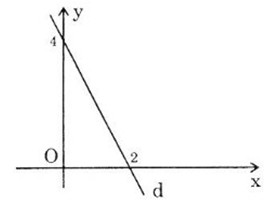
Đồ thị là đường thẳng đi qua \(2\) điểm:

+ Giao với trục tung \(P(0,4)\)

+ Giao với trục hoành \(Q(2, 0)\)

c) \(y = \sqrt {{x^2}} = |x| =\left\{ \matrix{- x,x \le 0 \hfill \cr x,x > 0 \hfill \cr} \right.\)

Bảng biến thiên

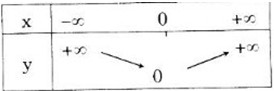
Đồ thị hàm số

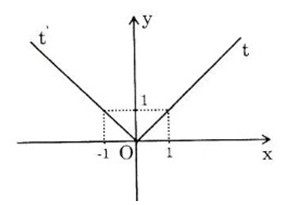
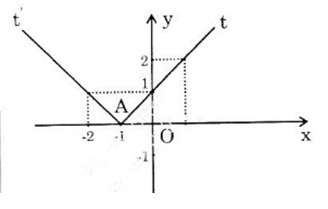
d) \(y = |x+1| = \left\{ \matrix{- x - 1,x \le - 1 \hfill \cr x + 1,x > - 1 \hfill \cr} \right.\)

Bảng biến thiên

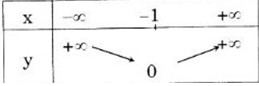
Đồ thị hàm số

Câu 10 trang 51 SGK Đại số 10

Lập bảng biến thiên và vẽ đồ thị của hàm số

a) \(y = x^2– 2x – 1\)

b) \(y = -x^2+ 3x + 2\)

Giải

a) \(y = x^2– 2x – 1\)

Tập xác định \(D =\mathbb R\)

Bảng biến thiên

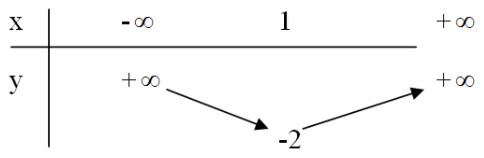
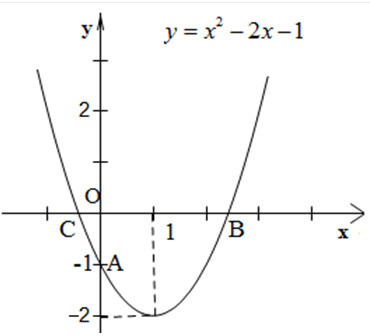
Đồ thị hàm số 

Đồ thị: parabol có đỉnh \(I(1; -2)\) với trục đối xứng \(x = 1\)

Giao điểm với trục tung là \(P(0;-1)\)

Giao điểm với trục hoành \(A (1-\sqrt2; 0)\) và \(B((1+\sqrt2; 0)\)

b) \(y = -x^2+ 3x + 2\)

Tập xác định \(D =\mathbb R\)

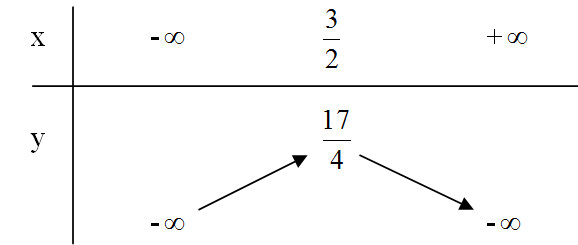
Đồ thị hàm số

Đồ thị: parabol có đỉnh \(I \left({3 \over 2},{{17} \over 4}\right)\)

với trục đối xứng \(x ={3 \over 2}\)

Giao điểm với trục tung là \(P(0,2)\)

Giao điểm với trục hoành \( A \left({{3 - \sqrt {17} } \over 2},0\right)\) và \(B\left({{3 + \sqrt {17} } \over 2},0\right)\)

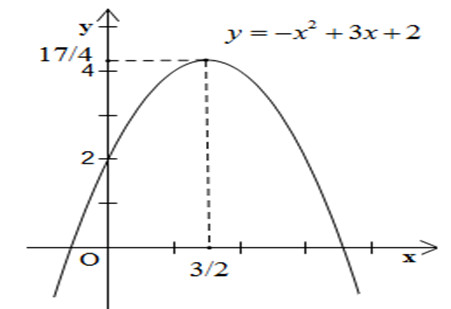
Câu 11 trang 51 SGK Đại số 10

Xác định \(a,b\), biết đường thẳng \(y = ax+ b\) đi qua hai điểm phân biệt \(A(1,3) , B(-1, 5)\)

Giải

\(A(1;3)\) thuộc đường thẳng \(y = ax + b\) nên tọa độ \(A\) là nghiệm đúng phương trình của đường thẳng, do đó ta có:

         \(3 = a.1+b \Leftrightarrow a+b=3\)           (1)

\(B(-1;5)\) thuộc đường thẳng \(y = ax + b\) nên tọa độ \(B\) là nghiệm đúng phương trình của đường thẳng, do đó ta có:

          \(5 = a.(-1) + b \Leftrightarrow -a+b=5\)   (2)

Giải hệ (1) và (2) ta được: \(a = -1, b = 4\)

Vậy phương trình đường thẳng cần tìm là: \(y=-x+4\)

Câu 12 trang 51 SGK Đại số 10

Tìm parabol \(y = ax^2+bx+c\), biết parabol đó

a) đi qua ba điểm \(A(0;-1), B(1; -1), C(-1; 1)\)

b) đi qua điểm \(D(3; 0)\) và có đỉnh \(I(1; 4)\)

Giải

a) Parabol \(y = ax^2+bx+c\) đi qua ba điểm \(A(0;-1), B(1; -1), C(-1; 1)\) nên tọa độ \(A,B,C\) thỏa mãn phương trình parabol ta được hệ phương trình:

\(\left\{ \matrix{
- 1 = a.0^2 + b.0 + c \hfill \cr
- 1 = a{.1^2} + b.1 + c \hfill \cr
1 = a{( - 1)^2} + b( - 1) + c \hfill \cr} \right.\)

⇔\(\left\{ \matrix{a = 1 \hfill \cr b = - 1 \hfill \cr c = - 1 \hfill \cr} \right.\)

Parabol có phương trình: \(y = x^2– x – 1\)

b) Parabol \(y = ax^2+bx+c\) đi qua điểm \(D(3; 0)\) và có đỉnh \(I(1; 4)\) nên ta có hệ:

\(\left\{ \matrix{
0 = a{.3^2} + b.3 + c \hfill \cr
1 = {{ - b} \over {2a}} \hfill \cr
4 = {{4ac - {b^2}} \over {4a}} \hfill \cr} \right.\)

⇔\(\left\{ \matrix{a = - 1 \hfill \cr b = 2 \hfill \cr c = 3 \hfill \cr} \right.\)

Phương trình parabol : \(y = -x^2+2x+3\)

Giaibaitap.me