Câu 27 trang 98 SGK Hình học 10

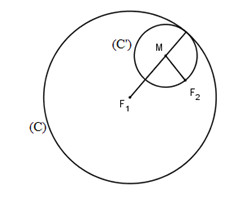
Cho đường tròn \((C)\) tâm \(F_1\) bán kính \(2a\) và một điểm \(F_2\) ở bên trong của \((C)\). Tập hợp điểm \(M\) của các đường tròn \((C’)\) thay đổi nhưng luôn đi qua \(F_2\) và tiếp xúc với \((C)\) (xem hình) là đường nào sau đây?

A. Đường thẳng                                                        

B. Đường tròn

C. Elip                                                                      

D. Parabol

Trả lời:

Gọi bán kính của đường tròn \((C’)\) là \(r\)

Ta có: \((C’)\) tiếp xúc trong với đường tròn \((C)\) nên \(F_1M = 2a – r\)

\(F_2 ∈ (C’)\) nên \(F_2M = r\)

Ta có: \(F_1M + F_2M = 2a – r + r = 2a\)

Suy ra: Tập hợp tâm \(M\) của đường tròn \((C’)\) là một elip

Vậy chọn C.

Câu 28 trang 98 SGK Hình học 10

Khi \(t\) thay đổi,  điểm \(M(5cost; 4sint)\) di động trên đường tròn nào sau đây:

A. Elip                                                 B. Đường thẳng

C. Parabol                                            D. Đường tròn

Trả lời:

Ta có:

\(\eqalign{
& x = 5\cos t \Rightarrow {x \over 5} = \cos t \Rightarrow {{{x^2}} \over {26}} = {\cos ^2}t \cr
& y = 4\sin t \Rightarrow {y \over 4} = \sin t \Rightarrow {{{y^2}} \over {16}} = {\sin ^2}t \cr
& \Rightarrow {{{x^2}} \over {25}} + {{{y^2}} \over {16}} = {\cos ^2}t + {\sin ^2}t \Rightarrow {{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1 \cr} \)

Vậy điểm \(M\) di động trên Elip \({{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1\)

Vậy chọn A.

Câu 29 trang 98 SGK Hình học 10

Cho elip \((E)\): \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1(0 < b < a)\). Gọi \(F_1,F_2\) là hai tiêu điểm và cho điểm \(M(0; -b)\)

Giá trị nào sau đây bằng giá trị của biểu thức : \(MF_1– MF_2– OM^2\)

A. \(c^2\)                                      B. \(2a^2\)                         

C. \(2b^2\)                                    D. \(a^2– b^2\)

Trả lời:

Elip \((E): {{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1(0 < b < a)\) , có hai tiêu điểm là \(F_1(-c; 0)\) và \(F_2(c; 0)\)

Với \(a^2= b^2+ c^2\)

Ta có \(MF_1 = a, MF_2= b\) và \(OM^2= b^2\)

\(MF_1MF_2 – OM^2= a^2– b^2\)

Vậy chọn D.

Câu 30 trang 98 SGK Hình học 10

Cho elip \((E) {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) :  và đường thẳng \(Δ: y + 3 = 0\)

Tích các khoảng cách từ hai tiêu điểm của \((E)\) đến đường thẳng \(Δ\) bằng các giá trị nào sau đây:

A. \(16\)                        B. \(9\)                          

C. \(81\)                        D. \(7\)

Trả lời:

Elip \((E) :{{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) :  có hai tiêu điểm \(F_1(-\sqrt7; 0)\) và \(F_2(\sqrt7; 0)\)

Khoảng cách từ \(F_1,F_2\) đến đường thẳng  \(Δ: y + 3 = 0\) là:

\(d(F_1, Δ)\) và \(d(F_2, Δ)\)

Suy ra: \(d(F_1, Δ).d(F_2, Δ)= 9\)

Vậy chọn B.

Giaibaitap.me