Câu 1 trang 98 SGK Hình học 10

Cho hai vecto \(a\) và \(b\) sao cho \(|\overrightarrow a | = 3;|\overrightarrow b | = 5;(\overrightarrow a ,\overrightarrow b ) = {120^0}\) . Với giá trị nào của m thì hai vecto \(\overrightarrow a  + m\overrightarrow b \) và \(\overrightarrow a  - m\overrightarrow b \) vuông góc với nhau?

Trả lời:

Để hai vecto \(\overrightarrow a  + m\overrightarrow b \) và \(\overrightarrow a  - m\overrightarrow b \) vuông góc với nhau thì:

\(\eqalign{
& (\overrightarrow a + m\overrightarrow b )(\overrightarrow a - m\overrightarrow b ) = 0 \cr
& \Leftrightarrow {(\overrightarrow a )^2} - m\overrightarrow a \overrightarrow b + m\overrightarrow a \overrightarrow b - {m^2}{(\overrightarrow b )^2} = 0 \cr
& \Leftrightarrow |\overrightarrow a {|^2} - m|\overrightarrow a ||\overrightarrow b |cos(\overrightarrow a ,\overrightarrow b ) + m|\overrightarrow a ||\overrightarrow b |cos(\overrightarrow a ,\overrightarrow b ) - {m^2}|\overrightarrow b | = 0 \cr
& \Leftrightarrow 9 + {{15} \over 2}m - {{15} \over 2}m - 25{m^2} = 0 \cr
& \Leftrightarrow 9 - 25{m^2} = 0 \Leftrightarrow m = \pm {3 \over 5} \cr} \)

Câu 2 trang 98 SGK Hình học 10

Cho tam giác \(ABC\) có hai điểm \(M,N\)  sao cho 

\(\left\{ \matrix{
\overrightarrow {AM} = \alpha \overrightarrow {AB} \hfill \cr
\overrightarrow {AN} = \beta \overrightarrow {AC} \hfill \cr} \right.\)

a) Hãy vẽ \(M, N\) khi \(\alpha  = {2 \over 3};\beta  =  - {2 \over 3}\)

b)  Hãy tìm mối liên hệ giữa \(α, β\) để \(MN//BC\)

Trả lời:

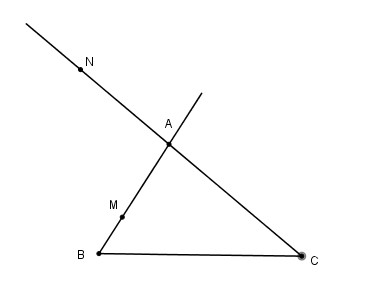
a) Ta có:

\(\eqalign{
& \overrightarrow {AM} = {2 \over 3}\overrightarrow {AB} \Leftrightarrow \left\{ \matrix{
\overrightarrow {AM} \uparrow \uparrow \overrightarrow {AB} \hfill \cr
AM = {2 \over 3}AB \hfill \cr} \right. \cr
& \overrightarrow {AN} = - {2 \over 3}\overrightarrow {AC} \Leftrightarrow \left\{ \matrix{
\overrightarrow {AN} \uparrow \downarrow \overrightarrow {AC} \hfill \cr
AN = {2 \over 3}AC \hfill \cr} \right. \cr} \)

b) Ta có:

\(\eqalign{
& \overrightarrow {AM} = \alpha \overrightarrow {AB} \cr
& \overrightarrow {AN} = \beta \overrightarrow {AC} \cr
& \Rightarrow \overrightarrow {AM} - \overrightarrow {AN} = \alpha \overrightarrow {AB} - \beta \overrightarrow {AC} \cr
& \Rightarrow \overrightarrow {MN} = \alpha \overrightarrow {AB} - \beta \overrightarrow {AC} \cr
& \Rightarrow \overrightarrow {MN} = \alpha (\overrightarrow {AB} - {\beta \over \alpha }\overrightarrow {AC} ),\alpha \ne 0 \cr} \)

Ta cũng có: \(\overrightarrow {BC}  =  - (\overrightarrow {AB}  - \overrightarrow {AC} )\)

Do đó, để \(MN // BC\) thì

\(\left\{ \matrix{
\overrightarrow {AB} - \overrightarrow {AC} \hfill \cr
\overrightarrow {AB} - {\beta \over \alpha }\overrightarrow {AC} \hfill \cr} \right.\)

 phải cùng phương, cho ta \({\beta  \over \alpha } = 1 \Rightarrow \alpha  = \beta \)

Câu 3 trang 99 SGK Hình học 10

 Cho tam giác đều \(ABC\) cạnh \(a\)

a) Cho \(M\) là một điểm trên đường tròn ngoại tiếp tam giác \(ABC\). Tính \(MA^2+ MB^2+ MC^2\) theo \(a\)

b) Cho đường thẳng \(a\) tùy ý, tìm điểm \(N\) trên đường thẳng \(d\) sao cho \(NA^2+ NB^2 + NC^2\) nhỏ nhất

Trả lời:

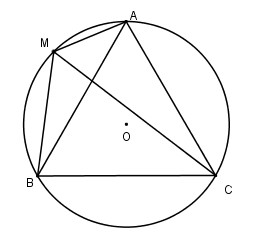
a) Ta có:

\(\eqalign{
& \overrightarrow {MA} = \overrightarrow {OA} - \overrightarrow {OM} \cr
& {\overrightarrow {MA} ^2} = {(\overrightarrow {OA} - \overrightarrow {OM} )^2} = {\overrightarrow {OA} ^2} + {\overrightarrow {OM} ^2} - 2\overrightarrow {OA} .\overrightarrow {OM} \cr
& \Rightarrow {\overrightarrow {MA} ^2} = 2{R^2} - 2\overrightarrow {OA} .\overrightarrow {OM} (1) \cr} \)

Tương tự ta có:

\(\eqalign{
& M{B^2} = {\overrightarrow {MB} ^2} = 2{R^2} - 2\overrightarrow {OB} .\overrightarrow {OM} (2) \cr
& M{C^2} = {\overrightarrow {MC} ^2} = 2{R^2} - 2\overrightarrow {OC.} \overrightarrow {OM} (3) \cr} \)

Từ (1), (2) và (3) suy ra:

 \(M{A^2} + M{B^2} + M{C^2} = 6{R^2} - 2\overrightarrow {OM} (\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} )\)

Tam giác \(ABC\) là tam giác đều nội tiếp đường tròn tâm \(O\) nên \(O\) cũng là trọng tâm của tam giác \(ABC\), cho ta \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} = \overrightarrow  0\)

Vậy \(M{A^2} + M{B^2} + M{C^2} = 6{R^2} \)

Vì đường tròn ngoại tiếp tam giác đều cạnh \(a\) nên ta có:

\(a = R\sqrt3   ⇒ 6R^2= 2(R\sqrt3)^2\)

Vậy  \(M{A^2} + M{B^2} + M{C^2}  = 2a^2\)

b) Gọi \(G\) là trọng tâm của tam giác ta có:

\(\eqalign{
& \overrightarrow {NA} = \overrightarrow {NG} + \overrightarrow {GA} \cr
& \Rightarrow {\overrightarrow {NA} ^2} = {\overrightarrow {GA} ^2} + 2\overrightarrow {NG} .\overrightarrow {GA} + {\overrightarrow {GA} ^2} \cr} \)

Tương tự ta có:

\(\eqalign{
& {\overrightarrow {NB} ^2} = {\overrightarrow {NG} ^2} + 2\overrightarrow {NG} .\overrightarrow {GB} + {\overrightarrow {GB} ^2} \cr
& {\overrightarrow {NC} ^2} = {\overrightarrow {NG} ^2} + 2\overrightarrow {NG} .\overrightarrow {GC} + {\overrightarrow {GC} ^2} \cr
& \Rightarrow N{A^2} + N{B^2} + N{C^2} = 3N{G^2} + 2\overrightarrow {NG} (\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} ) + G{A^2} + G{B^2} + G{C^2} \cr} \) 

Vì \(G\) là trọng tâm của tam giác

⇒ \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

\(\eqalign{
& {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2} = 3G{A^2} = 3.{({2 \over 3}.{{a\sqrt 3 } \over 2})^2} = {a^2} \cr
& \Rightarrow N{A^2} + N{B^2} + N{C^2} = {a^2} + 3N{G^2} \cr} \)

\(a^2\) là số không đổi nên tổng \(N{A^2} + N{B^2} + N{C^2}\) nhỏ nhất khi \(NG\) đạt giá trị nhỏ nhất. Vì \(NG\) là khoảng cách từ \(G\) đến điểm \(N\) thuộc đường thẳng \(d\) nên \(NG\) nhỏ nhất khi \(NG⊥d\) hay \(N\) là hình chiếu của trọng tâm \(G\) trên đường thẳng \(d\).

Câu 4 trang 99 SGK Hình học 10

Cho tam giác \(ABC\) đều có cạnh bằng \(6cm\). Một điểm \(M\) nằm trên cạnh \(BC\) sao cho \(BM  = 2cm\)

a) Tính độ dài của đoạn thẳng \(AM\) và tính cosin của góc \(BAM\)

b) Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\)

c) Tính độ dài đường trung tuyến vẽ từ \(C\) của tam giác \(ACM\)

d) Tính diện tích tam giác \(ABM\)

Trả lời:

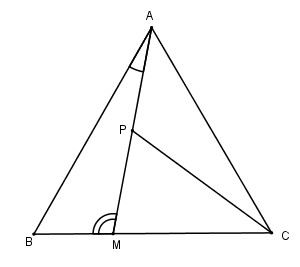
a) Ta có:

\(\eqalign{
& A{M^2} = B{A^2} + B{M^2} - 2BA.BM.\cos\widehat {ABM} \cr
& \Rightarrow A{M^2} = 36 + 4 - 2.6.2.{1 \over 2} \cr
& \Rightarrow A{M^2} = 28 \Rightarrow AM = 2\sqrt 7 (cm) \cr} \)

Ta cũng có:

\(\eqalign{
& \cos \widehat {BAM }= {{A{B^2} + A{M^2} - B{M^2}} \over {2AB.AM}} \cr
& \Rightarrow \cos\widehat { BAM }= {{5\sqrt 7 } \over {14}} \cr} \)

b) Trong tam giác \(ABM\), theo định lí Sin ta có:

\(\eqalign{
& {{AM} \over {\sin \widehat {ABM}}} = 2R \Leftrightarrow R = {{AM} \over {2\sin \widehat {ABM}}} \cr
& R = {{2\sqrt 7 } \over {2\sin {{60}^0}}} = {{2\sqrt {21} } \over 3}(cm) \cr} \)

c) Áp dụng công thức đường trung tuyến ta có:

\(\eqalign{
& C{P^2} = {{C{A^2} + C{M^2}} \over 2} - {{A{M^2}} \over 4} \cr
& \Rightarrow C{P^2} = {{36 + 16} \over 2} - {{28} \over 4} \cr
& \Rightarrow C{P^2} = 19 \Rightarrow CP = \sqrt {19} \cr}\)

d) Diện tích tam giác \(ABM\) là:

\(S = {1 \over 2}BA.BM\sin \widehat {ABM} = {1 \over 2}6.2\sin {60^0} = 3\sqrt 3 (c{m^2})\)

Giaibaitap.me