Bài 8 trang 12 sgk hình học lớp 10

Cho \(\left | \overrightarrow{a} +\overrightarrow{b}\right |= 0\). So sánh độ dài, phương và hướng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\)

Giải

Từ \(\left | \overrightarrow{a} +\overrightarrow{b}\right | = 0\), ta có \(\overrightarrow{a}+ \overrightarrow{b} = 0\) \(\Rightarrow \overrightarrow{a} = -\overrightarrow{b}\)

Điều này chứng tỏ hai vectơ có cùng độ dài \(\left | \overrightarrow{a} \right | = \left | \overrightarrow{b} \right |\), cùng phương và ngược hướng.

Bài 9 trang 12 sgk hình học lớp 10

Chứng minh rằng \(\overrightarrow{AB}= \overrightarrow{CD}\) khi và chỉ khi trung điểm của hai đoạn thẳng \(AD\)  và \(BC\) trùng nhau.

Giải

Ta chứng minh hai mệnh đề.

a) Cho  \(\overrightarrow{AB}\) = \(\overrightarrow{CD}\) thì \(AD\) và \(BC\) có trung điểm trùng nhau. Gọi \(I\) là trung điểm của \(AD\) ta chứng minh \(I\) cũng là trung điểm của \(BC\).

Theo quy tắc của ba điểm của tổng, ta có 

     \(\overrightarrow{AB}= \overrightarrow{AI} + \overrightarrow{IB}\);

      \(\overrightarrow{CD}= \overrightarrow{CI}+ \overrightarrow{ID}\)

Vì \(\overrightarrow{AB} = \overrightarrow{CD}\) nên \(\overrightarrow{AI} + \overrightarrow{IB}=  \overrightarrow{CI}+ \overrightarrow{ID}\)

                           \(\Rightarrow \overrightarrow{AI} - \overrightarrow{ID} = \overrightarrow{CI} - \overrightarrow{IB}\)

                           \(\Rightarrow\overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{CI} + \overrightarrow{BI}\)              (1)

Vì \(I\) là trung điểm của \(AD\) nên  \(\overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\)         (2)

Từ (1) và (2) suy ra \(\overrightarrow{CI} + \overrightarrow{BI} = \overrightarrow{0}\)                             (3)

Đẳng thức (3) chứng tỏ \(I\) là trung điểm của \(BC\).

b) \(AD\) và \(BC\)  có chung trung điểm \(I\), ta chứng minh \(\overrightarrow{AB}\) = \(\overrightarrow{CD}\).

\(I\) là trung điểm của \(AD\) \(\Rightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\)   \(\Rightarrow\overrightarrow{AI} - \overrightarrow{ID} =\overrightarrow{0}\)

\(I\) là trung điểm của \(BC\)  \(\Rightarrow \overrightarrow{CI} + \overrightarrow{BI}= \overrightarrow{0}\)    \(\Rightarrow \overrightarrow{CI} - \overrightarrow{IB}= \overrightarrow{0}\)

Suy ra  \(\overrightarrow{AI} - \overrightarrow{ID}=  \overrightarrow{CI}- \overrightarrow{IB}\) 

     \(\Rightarrow \overrightarrow{AI} + \overrightarrow{IB} = \overrightarrow{CI}+ \overrightarrow{ID}\)    \(\Rightarrow \overrightarrow{AB}= \overrightarrow{CD}\) (đpcm)

Bài 10 trang 12 sgk hình học lớp 10

Cho ba lực \(\overrightarrow {{F_1}}  = \overrightarrow {MA} ,\overrightarrow {{F_2}}  = \overrightarrow {MB} \) và \(\overrightarrow {{F_3}}  = \overrightarrow {MC} \) cùng tác động vào một vât tại điểm \(M\) và đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều là \(100N\)  và \(\widehat {AMB} = {60^0}\)

Tìm cường độ và hướng của lực \(\overrightarrow {{F_3}} \)

Giải

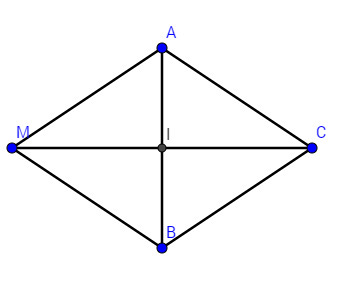
Theo đề bài cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều là \(100N\) nên \(MA=MB\). Mặt khác \(\widehat {AMB} = {60^0}\) nên tam giác \(ABM\) đều.

Do đó \( MI={{AM\sqrt 3 } \over 2} = {{100\sqrt 3 } \over 2} = 50\sqrt 3 \)

\(MC=2MI=2.50\sqrt 3=100\sqrt 3 \)

\(\overrightarrow {{F_3}}  = \overrightarrow {MC}  = \overrightarrow {MA}  + \overrightarrow {MB} \)

Do đó \(\overrightarrow {{F_3}} \) có hướng là tia phân giác trong của góc \(\widehat {AMB} \) và có độ lớn là \(100\sqrt 3 N\)

Giaibaitap.me