Bài 1 trang 17 sgk toán hình học lớp 10

Cho hình bình hành $ABCD$. Chứng mỉnh rằng:

 $\overrightarrow{AB} + \overrightarrow{AC}+ \overrightarrow{AD}= 2\overrightarrow{AC}$.

Giải

 $\overrightarrow{AB} + \overrightarrow{AC}+ \overrightarrow{AD}= \overrightarrow{AB}  + \overrightarrow{AD}+ \overrightarrow{AC}$

Vì $ABCD$ là hình bình hành nên

$\overrightarrow{AB}+ \overrightarrow{AD}= \overrightarrow{AC}$ (quy tắc hình bình hành của tổng)

$\Rightarrow \overrightarrow{AB}+ \overrightarrow{AC} + \overrightarrow{AD}=   \overrightarrow{AC} +\overrightarrow{AC} =2\overrightarrow{AC}$

Bài 2 trang 17 sgk hình học lớp 10

Cho $AK$ và $BM$ là hai trung tuyến của tam giác $ABC$. Hãy phân tích các vectơ $\overrightarrow {AB} ,\overrightarrow {BC} ,\overrightarrow {AC}$ theo hai vectơ sau $\overrightarrow u  = \overrightarrow {AK} ,\overrightarrow v  = \overrightarrow {BM}$

Giải

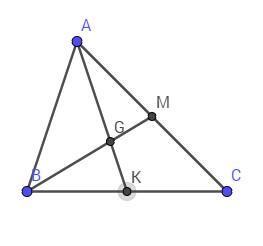
Gọi $G$ là giao điểm của $AK, BM$ thì $G$ là trọng tâm của tam giác.

Ta có : 

$\eqalign{ & \overrightarrow {AG} = {2 \over 3}\overrightarrow {AK} \Rightarrow \overrightarrow {AG} = {2 \over 3}\overrightarrow u \cr & \overrightarrow {GB} = - \overrightarrow {BG} = - {2 \over 3}\overrightarrow {BM} = - {2 \over 3}\overrightarrow v \cr}$

Theo quy tắc $3$ điểm đối với tổng vec tơ:

$\overrightarrow {AB}  = \overrightarrow {AG}  + \overrightarrow {GB}  \Rightarrow \overrightarrow {AB}  = {2 \over 3}\overrightarrow u  - {2 \over 3}\overrightarrow v  = {2 \over 3}(\overrightarrow u  - \overrightarrow v )$

$AK$ là trung tuyến thuộc cạnh $BC$ nên

$\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AK}  \Rightarrow {2 \over 3}\overrightarrow u  - {2 \over 3}\overrightarrow v  + \overrightarrow {AC}  = 2\overrightarrow u$

$\Rightarrow \overrightarrow {AC}  = {4 \over 3}\overrightarrow u  + {2 \over 3}\overrightarrow v  \Rightarrow \overrightarrow {CA}  =  - {4 \over 3}\overrightarrow u  - {2 \over 3}\overrightarrow v$

$BM$ là trung tuyến thuộc đỉnh $B$ nên 

$\eqalign{ & \overrightarrow {BA} + \overrightarrow {BC} = 2\overrightarrow {BM} \Rightarrow - \overrightarrow {AB} + \overrightarrow {BC} = 2\overrightarrow v \cr & \Rightarrow \overrightarrow {BC} = 2\overrightarrow v + {2 \over 3}\overrightarrow u - {2 \over 3}\overrightarrow v = {2 \over 3}\overrightarrow u + {4 \over 3}\overrightarrow v \cr}$

Bài 3 trang 17 sgk hình học lớp 10

 Trên đường thẳng chứa cạnh $BC$ của tam giác $ABC$ lấy một điểm $M$ sao cho $\overrightarrow {MB}  = 3\overrightarrow {MC}$. Hãy phân tích vectơ  $\overrightarrow {AM}$ theo hai vectơ $\overrightarrow u  = \overrightarrow {AB} ;\overrightarrow v  = \overrightarrow {AC}$

Giải

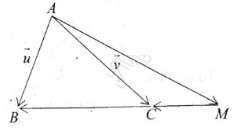
Trước hết ta có 

$\eqalign{ & \overrightarrow {MB} = 3\overrightarrow {MC} \Rightarrow \overrightarrow {MB} = 3.(\overrightarrow {MB} + \overrightarrow {BC} ) \cr & \Rightarrow \overrightarrow {MB} = 3\overrightarrow {MB} + 3\overrightarrow {BC} \cr & \Rightarrow - 2\overrightarrow {MB} = 3\overrightarrow {BC} \cr & \Rightarrow \overrightarrow {BM} = {3 \over 2}\overrightarrow {BC} \cr}$

mà $\overrightarrow {BC}  = \overrightarrow {AC}  - \overrightarrow {AB}$ nên $\overrightarrow {BM}  = {3 \over 2}(\overrightarrow {AC}  - \overrightarrow {AB} )$

Theo quy tắc $3$ điểm, ta có

$\eqalign{ & \overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + {3 \over 2}(\overrightarrow {AC} - \overrightarrow {AB} ) = - {1 \over 2}\overrightarrow {AB} + {3 \over 2}\overrightarrow {AC} \cr &\text{ Hay }  \overrightarrow {AM} = - {1 \over 2}\overrightarrow u + {3 \over 2}\overrightarrow v \cr}$

Bài 4 trang 17 sgk hình học lớp 10

Gọi $AM$ là trung tuyến của tam giác $ABC$  và $D$ là trung điểm của đạn $AM$. Chứng minh rằng:

a) $2\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = \overrightarrow 0$

b) $2\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = 4\overrightarrow {OD}$, với $O$ là điểm tùy ý.

Giải

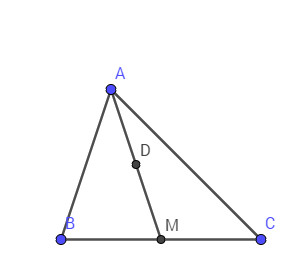
a) Vì $M$ là trung điểm của $BC$ nên:

Ta có:

$\overrightarrow {DB}  + \overrightarrow {DC}  = 2\overrightarrow {DM}$

Mặt khác, do $D$ là trung điểm của đoạn $AM$ nên $\overrightarrow {DM}  =  - \overrightarrow {DA}$

Khi đó: $2\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = 2\overrightarrow {DA}  + 2\overrightarrow {DM}  = 2\left( {\overrightarrow {DA}  + \overrightarrow {DM} } \right) = \overrightarrow 0$

b) Ta có:

$\eqalign{ & 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \cr & \Leftrightarrow 2\left( {\overrightarrow {OA} - \overrightarrow {OD} } \right) + \left( {\overrightarrow {OB} - \overrightarrow {OD} } \right) + \left( {\overrightarrow {OC} - \overrightarrow {OD} } \right) = \overrightarrow 0 \cr & \Leftrightarrow 2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \cr}$ (Đúng theo câu a) 

Vậy: $2\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = 4\overrightarrow {OD}$, với $O$ là điểm tùy ý

Giaibaitap.me