Bài 5 trang 17 sgk hình học lớp 10

Gọi \(M\) và \(N\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\) của tứ giác \(ABCD\). Chứng minh rằng:

                \(2\overrightarrow {MN}  = \overrightarrow {AC}  + \overrightarrow {BD}  = \overrightarrow {BC}  + \overrightarrow {AD} \)

Giải

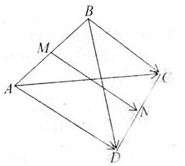
\(N\) là trung điểm của \(CD\):

           \(2\overrightarrow {MN}  = \overrightarrow {MC}  + \overrightarrow {MD} \)      (1)

Theo quy tắc 3 điểm, ta có:

           \(\overrightarrow {MC}  = \overrightarrow {MA}  + \overrightarrow {AC} \)            (2)

           \(\overrightarrow {MD}  = \overrightarrow {MB}  + \overrightarrow {BD} \)          (3)

Từ (1), (2), (3) ta có:

    \(2\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AC}  + \overrightarrow {MB}  + \overrightarrow {BD}  \)

\(= \left( {\overrightarrow {MA}  + \overrightarrow {MB} } \right) + \overrightarrow {AC}  + \overrightarrow {BD}  = \overrightarrow {AC}  + \overrightarrow {BD} \)

Chứng minh tương tự, ta có: \(2\overrightarrow {MN}  = \overrightarrow {BC}  + \overrightarrow {AD} \)

Bài 6 trang 17 sgk hình học lớp 10

 Cho hai điểm phân biệt \(A\) và \(B\). Tìm điểm \(K\) sao cho

                        \(3\overrightarrow{KA} + 2\overrightarrow{KB} = \overrightarrow{0}\).

Giải

Ta có:   \(3\overrightarrow{KA} + 2\overrightarrow{KB} = \overrightarrow{0}\)\( \Rightarrow  3\overrightarrow{KA}= -2 \overrightarrow{KB}\) \( \Rightarrow \overrightarrow{KA} = - \frac{2}{3}\overrightarrow{KB}\)

Đẳng thức này chứng tỏ hi vec tơ  \(\overrightarrow{KA},\overrightarrow{KB}\) là hai véc tơ ngược hướng, do đó \(K\) thuộc đoạn \(AB\)

Ta lại có: \(\left | \overrightarrow{KA} \right |= \frac{2}{3}\left | \overrightarrow{KB} \right |\)\( \Rightarrow  KA = \frac{2}{3} KB\)

Vậy \(K\) là điểm chia trong đoạn thẳng \(AB\) theo tỉ số \(\frac{2}{3}\).

Bài 7 trang 17 sgk hình học lớp 10

Cho tam giác \(ABC\). Tìm điểm \(M\) sao cho \(\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \overrightarrow 0 \)

Giải

Gọi \(D\) là trung điểm của cạnh \(AB\), ta có:

\(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MD} \)

Đẳng thức đã cho trở thành:

\(2\overrightarrow {MD}  + 2\overrightarrow {MC}  = \overrightarrow 0 \)

\(\Rightarrow \overrightarrow {MD}  + \overrightarrow {MC}  = \overrightarrow 0 \)

Đẳng thức này chứng tỏ \(M\) là trung điểm của \(CD\)

Bài 8 trang 17 sgk hình học lớp 10

Cho lục giác \(ABCDEF\). Gọi \(M, N, P, Q, R, S\) lần lượt là trung điểm của các cạnh \(AB, BC, CD, DE, EF, FA\). Chứng minh rằng hai tam giác \(MPR\) và \(NQS\) có cùng trọng tâm.

Giải

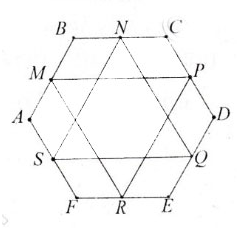
\(MN\) là đường trung bình của tam giác \(ABC\) nên ta có:

      \(\overrightarrow {MN}  = {1 \over 2}\overrightarrow {AC} \)

Tương tự ta có:        

  \(\eqalign{
& \overrightarrow {PQ} = {1 \over 2}\overrightarrow {CE} \cr
& \overrightarrow {RS} = {1 \over 2}\overrightarrow {EA} \cr} \)

\(\eqalign{
& \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = {1 \over 2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right) = {1 \over 2}\overrightarrow {AA} = \overrightarrow 0 \cr
& \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0 (1) \cr
& \cr} \)   

Gọi \(G\) là trong tâm của tam giác \(MPR\), ta có:

        \(\overrightarrow {GM}  + \overrightarrow {GP}  + \overrightarrow {GR}  = \overrightarrow 0 (2)\)

Mặt khác : 

\(\eqalign{
& \overrightarrow {MN} = \overrightarrow {MG} + \overrightarrow {GN} \cr
& \overrightarrow {PQ} = \overrightarrow {PG} + \overrightarrow {GQ} \cr
& \overrightarrow {RS} = \overrightarrow {RG} + \overrightarrow {GS} \cr} \)

\(\Rightarrow \overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RS}  = \left( {\overrightarrow {MG}  + \overrightarrow {PG}  + \overrightarrow {RG} } \right) + \overrightarrow {GN}  + \overrightarrow {GQ}  + \overrightarrow {GS} (3)\)

Từ (1),(2), (3) suy ra: \(\overrightarrow {GN}  + \overrightarrow {GQ}  + \overrightarrow {GS}  = \overrightarrow 0 \)

Vậy \(G\) là trọng tâm của tam giác \(NQS\)

Bài 9 trang 17 sgk hình học lớp 10

Cho tam giác đều \(ABC\) có trọng tâm \(O\) và \(M\) là một điểm tùy ý trong tam giác. Gọi \(D,E,F\) lần lượt là chân đường vuông góc hạ từ \(M\) đến \(BC, AC, AB\). Chứng minh rằng:

          \(\overrightarrow {MD}  + \overrightarrow {ME}  + \overrightarrow {MF}  = {3 \over 2}\overrightarrow {MO} \)

Giải

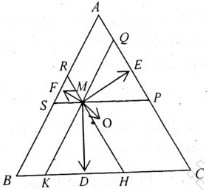
Qua M kẻ các đường thẳng song song với các cạnh của tam giác

A₁B₁ // AB;  A₂C₂ // AC;   B₂C₁ // BC.

Dễ thấy các tam giác MB₁C₂; MA₁C₁;MA₂B₂ đều là các tam giác đều. Ta lại có MD 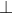B₁C₂ nên MD cũng là trung điểm thuộc cạnh B₁C₂ của tam giác MB₁C₂

Ta có 2 = +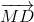 

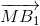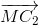
Tương tự: 2 = +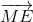 

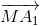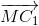
               2 = +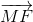

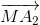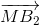
=> 2( ++) = (+) + ( + ) + (+)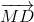

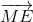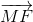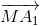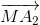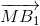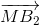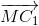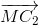Tứ giác là hình bình hành nên

           +  = 

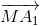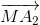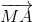
Tương tự: + =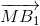 

                 + = 

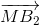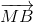
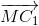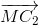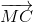
=> 2( ++) = ++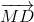

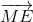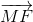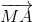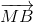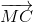
vì O là trọng tâm bất kì của tam giác và M là một điểm bất kì nên

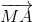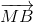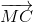 ++ = 3.

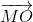Cuối cùng ta có: 

2( 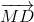++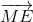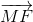) = 3;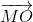

=>  ++ = 

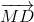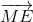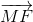Giaibaitap.me