Bài 5 trang 27 sgk hình học lớp 10

Trong các mặt phẳng \(Oxy\) cho điểm \((x_0; y_0)\)

a) Tìm tọa độ điểm \(A\) đối xứng với \(M\) qua trục \(Ox\);

b) Tìm tọa độ điểm \(B\) đối xứng với \(M\) qua trục \(Oy\);

c) Tìm tọa độ điểm \(C\) đối xứng với \(M\) qua gốc \(O\).

Giải

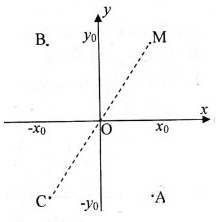
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.

  \({M}({x_0};{y_0}) \Rightarrow {A}({x_0}; - {y_0})\)

b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.

  \({M}({x_0};{y_0}) \Rightarrow {B}( - {x_0};{y_0})\)

c) Hai điểm đối xứng nhau qua gốc \(O\) thì các tọa độ tương ứng đối nhau.

  \(M({x_0};{y_0}) \Rightarrow C( - {x_0}; - {y_0})\)

Bài 6 trang 27 sgk hình học lớp 10

Cho hình bình hành \(ABCD\) có \(A(-1; -2), B(3;2), C(4;-1)\). Tìm tọa độ điểm \(D.\)

Giải

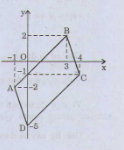
Tứ giác \(ABCD\) là hình bình hành nên 

\(\overrightarrow{CD}=\overrightarrow{BA}\) 

Gọi \((x; y)\) là tọa độ của \(D\) thì

\(\overrightarrow{CD} = (x-4; y+1)\)

\(\overrightarrow{BA}= (-4;-4)\)

\(\overrightarrow{CD}\) = \(\overrightarrow{BA}\)  ⇔ \(\left\{\begin{matrix} x-4 = -4\\ y+1 = -4 \end{matrix}\right.\)  ⇔ \(\left\{\begin{matrix} x=0\\ y=-5 \end{matrix}\right.\)

Vậy điểm \(D(0;-5)\) là điểm cần tìm.

Bài 7 trang 27 sgk hình học lớp 10

Các điểm \(A'(-4; 1), B'(2;4), C'(2, -2)\) lần lượt là trung điểm của các cạnh \(BC, CA\) và \(AB\) của tam giác \(ABC\). Tính tọa độ đỉnh của tam giác \(ABC\). Chứng minh rằng trọng tâm tam giác \(ABC\) và \(A'B'C'\) trùng nhau.

Giải

Giả sử \(A({x_A};{y_A}),B({x_B};{y_B}),C({x_C};{y_C})\)

\(A'\) là trung điểm của cạnh \(BC\) nên \(-4 = \frac{1}{2} (x_B+ x_C)\)

\(\Rightarrow {x_B} + {x_C} =  - 8\)                       (1)

Tương tự ta có \({x_A} + {x_C} = 4\)       (2)

                       \({x_B} + {x_A} = 4\)         (3)  

Giải hệ (1), (2) và (3) ta được:

       \(\left\{ \matrix{
{x_A} = 8 \hfill \cr
{x_B} = - 4 \hfill \cr
x{}_C = - 4 \hfill \cr} \right.\)

Tương tự ta tính được:

      \(\left\{ \matrix{
{y_A} = 1 \hfill \cr
{y_B} = - 5 \hfill \cr
y{}_C = 7 \hfill \cr} \right.\)

Gọi \(G({x_G};y{}_G)\) là trọng tâm của tam giác \(ABC\)

Khi đó ta có:

$$\left\{ \matrix{
{x_G} = {{{x_A} + {x_B} + {x_C}} \over 3} = {{8 - 4 - 4} \over 3} = 0 \hfill \cr
{y_G} = {{{y_A} + {y_B} + y{}_C} \over 3} = {{1 - 5 + 7} \over 3} = {1} \hfill \cr} \right.$$ 

Vậy \(G(0;1)\)  (*)

Gọi \(G'({x_{G'}};y{}_{G'})\) là trong tâm của tam giác \(A'B'C'\)

Khi đó ta có:

$$\left\{ \matrix{
{x_{G'}} = {{{x_{A'}} + {x_{B'}} + {x_{C'}}} \over 3} = {{ - 4 + 2 + 2} \over 3} = 0 \hfill \cr
{y_{G'}} = {{{y_{A'}} + {y_{B'}} + y{}_{C'}} \over 3} = {{1 + 4 - 2} \over 3} = 1 \hfill \cr} \right.$$

Vậy \(G'(0;1)\)  (2*)

Từ (*) và (2*) ta thấy \(G \equiv G'\)

Vậy trọng tâm tam giác \(ABC\) và \(A'B'C'\) trùng nhau.

Bài 8 trang 27 sgk hình học lớp 10

Cho \(\overrightarrow{a}= (2; -2)\), \(\overrightarrow{b} = (1; 4)\). Hãy phân tích vectơ \(\overrightarrow{c} = (5; 0)\) theo hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\)

Giải

 Giả sử ta phân tích được \(\overrightarrow{c}\) theo \(\overrightarrow{a}\) và \(\overrightarrow{b}\) tức là có hai số \(m, n\) để 

\(\overrightarrow{c}= m.\overrightarrow{a} + n.\overrightarrow{b}\) cho ta \(\overrightarrow{c}= (2m+n; -2m+4n)\)

Vì \(\overrightarrow{c} =(0;5)\) nên ta có hệ: \(\left\{\begin{matrix} 2m+n=5\\ -2m+4n=0 \end{matrix}\right.\)
Giải hệ phương trình ta được \(m = 2, n = 1\)

Vậy \(\overrightarrow{c} = 2\overrightarrow{a} + \overrightarrow{b}\)

Giaibaitap.me