Câu 5 trang 27 SGK Hình học 10
Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \(O\). Hãy xác định các điểm \(M, N, P\) sao cho:
a) \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \)
b) \(\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \)
c) \(\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} \)
Trả lời:
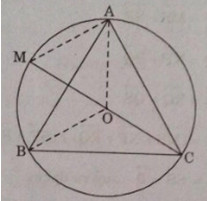
a) Nối \(OC\) và kéo dài cắt đường tròn tại điểm \(M\)
Dễ thấy, tam giác \(OAM\) là tam giác đều và \(OAMB\) là hình bình hành, cho ta:
\(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OM} \)
b) Nối \(OB\) và kéo dài cắt đường tròn tại điểm \(P\)
Tương tự như trên ta có:
\(\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \)
c) Nối \(OA\) và kéo dài cắt đường tròn tại điểm \(N\)
Tương tự như trên ta có:
\(\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} \)
Câu 6 trang 27 SGK Hình học 10
Cho tam giác đều \(ABC\) có cạnh bằng \(a\). Tính:
a) \(|\overrightarrow {AB} + \overrightarrow {AC} |\)
b) \(|\overrightarrow {AB} - \overrightarrow {AC} |\)
Trả lời:
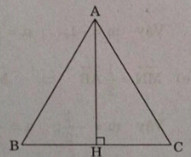
a) Hạ \(AH\bot BC\) do tam giác \(ABC\) đều nên \(H\) là trung điểm của \(BC\)
Ta có:
\(\eqalign{
& \overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AH} \cr
& \Rightarrow |\overrightarrow {AB} + \overrightarrow {AC} | = 2|\overrightarrow {AH} | = 2AH \cr} \)
Mà \(AH = {{a\sqrt 3 } \over 2} \Rightarrow |\overrightarrow {AB} + \overrightarrow {AC} | = a\sqrt 3 \)
b) \(|\overrightarrow {AB} - \overrightarrow {AC} | = |\overrightarrow {CB} | = a\)
Giaibaitap.me
Giải bài tập trang 28 bài ôn tập chương I - Vectơ Sách giáo khoa (SGK) Hình học 10. Câu 7: Cho sáu điểm...
Giải bài tập trang 27 bài ôn tập chương I - Vectơ Sách giáo khoa (SGK) Hình học 10. Câu 11: Tìm m để hai vectơ cùng phương...
Giải bài tập trang 29 bài ôn tập chương I - Vectơ Sách giáo khoa (SGK) Hình học 10. Câu 1: Cho tứ giác ...
Giải bài tập trang 29 bài ôn tập chương I - Vectơ Sách giáo khoa (SGK) Hình học 10. Câu 5: Cho ba điểm phân biệt ...
