Câu 5 trang 29 SGK Hình học 10

Cho ba điểm phân biệt $A, B, C$. Đẳng thức nào sau đây là đúng?

A. $\overrightarrow {CA}  - \overrightarrow {BA}  = \overrightarrow {BC}$

B. $\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {BC}$

C. $\overrightarrow {AB}  + \overrightarrow {CA}  = \overrightarrow {CB}$                                             

D. $\overrightarrow {AB}  - \overrightarrow {BC}  = \overrightarrow {CA}$    

Trả lời:

Với ba điểm $A, B, C$ ta có:

$\eqalign{ & \overrightarrow {CA} - \overrightarrow {BA} = \overrightarrow {CA} + \overrightarrow {AB} = \overrightarrow {CB} \ne \overrightarrow {BC} \cr  & \overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} \Leftrightarrow \overrightarrow {AB} = \overrightarrow {BC} - \overrightarrow {AC} = \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {BA} \cr  & \Rightarrow A \equiv B \cr}$

(trái với giả thiết)

$\eqalign{ & \overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \cr  & \overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {CA} \Leftrightarrow \overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {CA} \cr  & \Rightarrow A \equiv B \cr}$

  ⇒ trái với giả thiết

c) đúng vì $\overrightarrow {AB}  + \overrightarrow {CA}  = \overrightarrow {CA}  + \overrightarrow {AB}  = \overrightarrow {CB}$

Vậy chọn C

Câu 6 trang 29 SGK Hình học 10

Cho hai điểm phân biệt $A$ và $B$. Điều kiện để điểm $I$ là trung điểm của đoạn thẳng $AB$ là:

a) $IA = IB$                                    

b) $\overrightarrow {IA}  = \overrightarrow {IB}$

c) $\overrightarrow {IA}  =  - \overrightarrow {IB}$

 d) $\overrightarrow {AI}  = \overrightarrow {BI}$

Trả lời:

c) đúng. Vì:

$\overrightarrow {IA}  =  - \overrightarrow {IB}  \Leftrightarrow \overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0$

$⇔ I$ là trung điểm của đoạn thẳng $AB$

Câu 7 trang 29 SGK Hình học 10

Cho tam giác $ABC$ có $G$ là trọng tâm, $I$ là trung điểm của đoạn thẳng $BC$. Đẳng thức nào sau đây là đúng?

A. $\overrightarrow {GA}  = 2\overrightarrow {GI}$                                               

B. $\overrightarrow {IG}  =  - {1 \over 3}\overrightarrow {IA}$

C. $\overrightarrow {GB}  + \overrightarrow {GC}  = 2\overrightarrow {GI}$                                      

D. $\overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow {GA}$            

Trả lời:

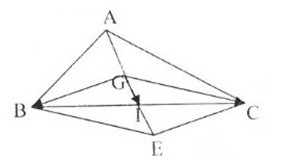
$I$ là trung điểm của $BC$ và $G$ là trọng tâm của tam giác $ABC$,

Gọi $E$ là điểm đối xứng với $G$ qua $I$  thì tứ giác $BGCE$ là hình bình hành

Suy ra: $\overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow {GE}  = 2\overrightarrow {GI}$

Câu 8 trang 29 SGK Hình học 10

Cho hình bình hành $ABCD$. Đẳng thức nào sau đây là đúng?

A. $\overrightarrow {AC}  + \overrightarrow {BD}  = 2\overrightarrow {BC}$                                             

B. $\overrightarrow {AC}  + \overrightarrow {BC}  = \overrightarrow {AB}$

C. $\overrightarrow {AC}  - \overrightarrow {BD}  = 2\overrightarrow {CD}$                                              

D. $\overrightarrow {AC}  - \overrightarrow {AD}  = \overrightarrow {CD}$

Trả lời:

Ta có: tứ giác $ABCD$ là hình bình hành nên:

$\left\{ \matrix{ \overrightarrow {AB} = \overrightarrow {DC} \hfill \cr \overrightarrow {AD} = \overrightarrow {BC} \hfill \cr} \right.$

$\eqalign{ & \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} +\overrightarrow {AD}+ \overrightarrow {BC} + \overrightarrow {CD} = 2\overrightarrow {BC} \cr & \overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {BC} = \overrightarrow {AB} + 2\overrightarrow {BC} \ne \overrightarrow {AB} \cr & \overrightarrow {AC} - \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {BC} - \overrightarrow {BC} - \overrightarrow {CD} = \overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {AB} \ne 2\overrightarrow {CD} \cr & \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} - \overrightarrow {BC} = \overrightarrow {AB} \ne \overrightarrow {CD} \cr}$

Vậy A đúng.

Giaibaitap.me