Câu 1 trang 28 SGK Hình học 10
Cho tứ giác \(ABCD\). Số các vectơ khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là bốn đỉnh của tứ giác bằng:
a) \(4\) b) \(6\)
c) \(8\) d) \(12\)
Trả lời
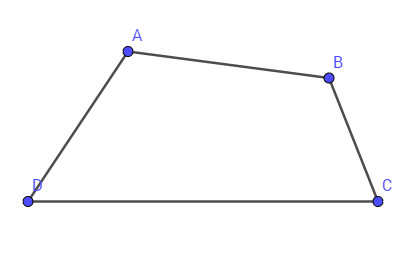
Từ mỗi điểm, ta nối với \(3\) điểm còn lại để có được \(3\) đoạn thẳng.
Vậy ta có : \(3.4 = 12\)
Do đó: d) đúng
Ta có \(12\) vectơ là: \(\overrightarrow {AB} ;\overrightarrow {BA} ;\overrightarrow {AC} ;\overrightarrow {CA} ;\overrightarrow {AD} ;\overrightarrow {DA} ;\overrightarrow {BD} ;\)
\(\overrightarrow {DB} ;\overrightarrow {BC} ;\overrightarrow {CB} ;\overrightarrow {CD} ;\overrightarrow {DC} \)
Câu 2 trang 29 SGK Hình học 10
Cho lục giác đều \(ABCDEF\) tâm \(O\). Số các vecto khác \(\overrightarrow 0 \) cùng phương với \(\overrightarrow {OC} \) có điểm đầu và điểm cuối là các đỉnh của lục giác bằng:
a) \(4\) b) \(6\)
c) \(7\) d) \(8\)
Trả lời:

a) Đúng
Ta có \(4\) vectơ cùng phương với mà điểm đầu và điểm cuối là đỉnh của lục giác: \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {ED} ,\overrightarrow {DE} \)
Câu 3 trang 29 SGK Hình học 10
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Số các vectơ bằng vectơ \(\overrightarrow {OC} \) có điểm đầu và điểm cuối là các đỉnh của lục giác là:
a) \(2\) b) \(3\)
c) \(4\) d) \(6\)
Trả lời:
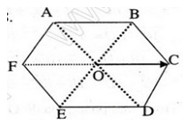
Các vecto khác có điểm đầu và điểm cuối là đỉnh của lục giác đều bằng \(\overrightarrow {OC} \) là:
\(\overrightarrow {FO} ,\overrightarrow {AB} ,\overrightarrow {ED} \)
Vậy số vecto là \(3\). Do đó chọn b.
Câu 4 trang 29 SGK Hình học 10
Cho hình chữ nhật \(ABCD\) có \(AB = 3, BC = 4\). Độ dài của vectơ \(\overrightarrow {AC} \) là:
a) \(5\) b) \(6\)
c) \(7\) d) \(9\)
Trả lời:

Ta có: \(ABCD\) là hình chữ nhật
\(\eqalign{
& \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \Rightarrow |\overrightarrow {AC} | = |\overrightarrow {AB} + \overrightarrow {BC} | \cr
& \Rightarrow |\overrightarrow {AC} | = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {4^2}} = 5 \cr} \)
Vậy chọn A.
Giaibaitap.me
Giải bài tập trang 29 bài ôn tập chương I - Vectơ Sách giáo khoa (SGK) Hình học 10. Câu 5: Cho ba điểm phân biệt ...
Giải bài tập trang 29, 30 bài ôn tập chương I - Vectơ Sách giáo khoa (SGK) Hình học 10. Câu 9: Trong mặt phẳng tọa độ...
Giải bài tập trang 30 bài ôn tập chương I - Vectơ Sách giáo khoa (SGK) Hình học 10. Câu 11: Cho tam giác...
Giải bài tập trang 30, 31 bài ôn tập chương I - Vectơ Sách giáo khoa (SGK) Hình học 10. Câu 15: Khẳng định nào sau đây là đúng...
