Bài 5 trang 12 sgk hình học lớp 10

Cho tam giác \(ABC\) cạnh \(a\). Tính độ dài của các vectơ \(\overrightarrow{AB}+ \overrightarrow{BC}\) và \(\overrightarrow{AB}- \overrightarrow{BC}\)

Giải

Ta có \(\overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}\)

\(\left | \overrightarrow{AB}+\overrightarrow{BC} \right | = \left | \overrightarrow{AC} \right |= a\)

Ta có: \(\overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{AB} +\overrightarrow{CB}\).

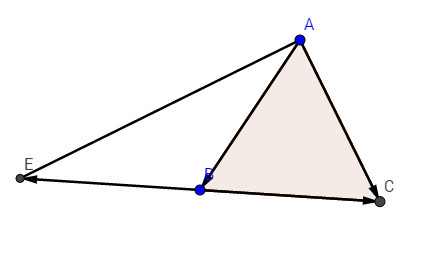
Trên tia \(CB\), ta dựng \(\overrightarrow{BE} = \overrightarrow{CB}\)

\( \Rightarrow \overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{AB} +\overrightarrow{BE}= \overrightarrow{AE}\)

Tam giác \(EAC\) vuông tại \(A\) (vì có đường trung tuyến \(AB\) bằng nửa cạnh \(CE\)) có : \(AC = a, CE = 2a\) , suy ra \(AE = \sqrt {C{E^2} - A{C^2}}  = \sqrt {4{a^2} - {a^2}}  = a\sqrt 3 \)

Vậy \(\left | \overrightarrow{AB } -\overrightarrow{BC}\right | = \left | \overrightarrow{AE} \right | = a\sqrt3\)

Bài 6 trang 12 sgk hình học lớp 10

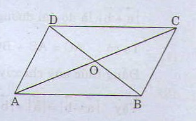
Cho hình bình hành \(ABCD\) có tâm \(O\). Chứng minh rằng:

a) \(\overrightarrow{CO} - \overrightarrow{OB} = \overrightarrow{BA}\);

b) \(\overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{DB}\);

c) \(\overrightarrow{DA}  -\overrightarrow{DB} = \overrightarrow{OD} - \overrightarrow{OC}\);

d) \(\overrightarrow{DA} - \overrightarrow{DB} + \overrightarrow{DC} = \overrightarrow{0}\).

Giải

a) Ta có, theo quy tắc ba điểm của phép trừ:

                     \(\overrightarrow{BA} = \overrightarrow{OA}- \overrightarrow{OB}\)     (1)

Mặt khác,        \(\overrightarrow{OA} = \overrightarrow{CO}\)                (2)

Từ (1) và (2) suy ra:

\(\overrightarrow{BA}= \overrightarrow{CO} - \overrightarrow{OB}\).

b) Ta có : \(\overrightarrow{DB}= \overrightarrow{AB} - \overrightarrow{AD}\)                 (1)

                \(\overrightarrow{AD} = \overrightarrow{BC}\)                             (2)

Từ (1) và (2) cho ta:

\(\overrightarrow{DB} = \overrightarrow{AB}- \overrightarrow{BC}\).

c) Ta có :

\(\overrightarrow{DA} - \overrightarrow{DB} = \overrightarrow{BA}\)           (1)

\(\overrightarrow{OD} - \overrightarrow{OC} = \overrightarrow{CD}\)            (2)

\(\overrightarrow{BA} = \overrightarrow{CD}\)                        (3)

Từ (1), (2), (3) suy ra

\(\overrightarrow{DA}  -\overrightarrow{DB} = \overrightarrow{OD} - \overrightarrow{OC}\) đpcm.

d) \(\overrightarrow{DA} - \overrightarrow{DB} + \overrightarrow{DC} = (\overrightarrow{DA} - \overrightarrow{DB}) + \overrightarrow{DC}\)

\(= \overrightarrow{BA}+\overrightarrow{DC} = \overrightarrow{BA}+ \overrightarrow{AB}= \overrightarrow{0}\) ( vì \(\overrightarrow{DC}= \overrightarrow{AB}) \).

Bài 7 trang 12 sgk hình học lớp 10

Cho \(\overrightarrow{a}\), \(\overrightarrow{b}\) là hai vectơ khác\(\overrightarrow{0}\). Khi nào có đẳng thức

a) \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |\) + \(\left | \overrightarrow{b} \right |\);

b)  \(\left | \overrightarrow{a}+\overrightarrow{b} \right |= \left | \overrightarrow{a}-\overrightarrow{b} \right |\).

Giải

a) Ta có  \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |\) + \(\left | \overrightarrow{b} \right |\)

Nếu coi hình bình hành \(ABCD\) có \(\overrightarrow{AB} = \overrightarrow{DC}= \overrightarrow{a}\) và \(\overrightarrow{AD}= \overrightarrow{BC}= \overrightarrow{b}\) thì  \(\left | \overrightarrow{a}+\overrightarrow{b} \right |\) là độ dài đường chéo \(AC\) và \(\left | \overrightarrow{a} \right |= AB\); \(\left | \overrightarrow{b} \right |= BC\).

Ta lại có: \(AC = AB + BC\)

Đẳng thức xảy ra khi điểm \(B\) nằm giữa hai điểm \(A, C\).

Vậy  \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |+ \left | \overrightarrow{b} \right |\) khi hai vectơ \(\overrightarrow{a}\), \(\overrightarrow{b}\) cùng hướng.

b) Tương tự, \(\left | \overrightarrow{a}+\overrightarrow{b} \right |\) là độ dài đường chéo \(AC\)

                     \(\left | \overrightarrow{a}-\overrightarrow{b} \right |\) là độ dài đường chéo \(BD\)

                     \(\left | \overrightarrow{a}+\overrightarrow{b} \right | =\left | \overrightarrow{a}-\overrightarrow{b} \right |\) \(\Rightarrow AC = BD\).

Hình bình hành \(ABCD\) có hai đường chéo bằng nhau nên nó là hình chữ nhật, ta có \(AD \perp AB\)  hay \(\overrightarrow{a}\perp\overrightarrow{b}\).

Giaibaitap.me