Câu 1 trang 27 SGK Hình học 10

Cho lục giác đều \(ABCDEF\) có tâm \(O\). Hãy chỉ ra các vectơ bằng \(\overrightarrow {AB} \) có điểm đầu và điểm cuối là \(O\) hoặc các đỉnh của lục giác.

Trả lời:

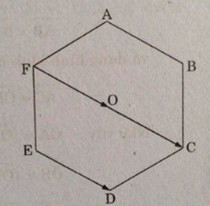
Trên hình vẽ, ta thấy các vecto: \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \) là các vectơ bằng \(\overrightarrow {AB} \).

Câu 2 trang 27 SGK Hình học 10

Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \) . Các khẳng định sau đúng hay sai?

A. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)  cùng hướng thì cùng phương

B. Hai vectơ \(\overrightarrow b \) và \(k\overrightarrow b \) cùng phương

C. Hai vectơ \(\overrightarrow a \) và \(( - 2)\overrightarrow a \) cùng hướng

D. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \) ngược hướng với vectơ thứ ba khác \(\overrightarrow 0 \)  thì  cùng phương.

Trả lời:

a) Đúng, vì ta chỉ xét các vectơ cùng hướng hay ngược hướng khi các vectơ này cùng phương.

b) Đúng (theo định nghĩa tích của một số với một vectơ)

c) Sai, \(\overrightarrow a \) và \(( - 2)\overrightarrow a \)  là hai vectơ ngược hướng

d) Đúng.

Câu 3 trang 27 SGK Hình học 10

 Tứ giác \(ABCD\) là hình gì nếu \(\overrightarrow {AB}  = \overrightarrow {DC} \) và \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\)

Trả lời:

Ta có:

\(\overrightarrow {AB}  = \overrightarrow {DC} \) suy ra \(AB//DC\) và \(AB=DC\) do đó \(ABCD\) là hình bình hành                     

\(|\overrightarrow {AB} | = |\overrightarrow {BC} |\) suy ra \(AB=BC\), hình bình hành \(ABCD\) có \(2\) cạnh liên tiếp bằng nhau do đó \(ABCD\) là hình thoi (theo dấu hiệu nhận biết hình thoi).

Câu 4 trang 27 SGK Hình học 10

Chứng minh rằng \(|\overrightarrow a  + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow {b|} \)

Trả lời: 

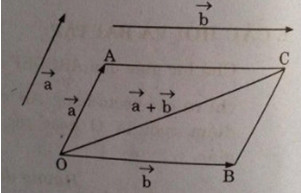
Từ một điểm \(O\) trong mặt phẳng ta dựng vectơ:

\(\eqalign{
& \overrightarrow {OA} = \overrightarrow a \cr
& \overrightarrow {OB} = \overrightarrow b \cr} \)

Và dựng hình bình hành \(OACB\) \( \Rightarrow \overrightarrow {AC}  = \overrightarrow {OB} \)

Như vậy:

\(\eqalign{
& OA = |\overrightarrow {OA} | = |\overrightarrow a | \cr
& OB = |\overrightarrow {OB} | = |\overrightarrow b | \Rightarrow AC = |\overrightarrow {AC} | = |\overrightarrow b | \cr
& \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \Rightarrow \overrightarrow {OC} = \overrightarrow a + \overrightarrow b \cr
& OC = |\overrightarrow {OC} | = |\overrightarrow a + \overrightarrow b | \cr} \)

Áp dụng bất đẳng thức tam giác vào tam giác \(OAC\), ta có:

\(OA + AC ≥ OC         ⇒ |\overrightarrow a  + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow {b|} \).

Giaibaitap.me