Bài 4 trang 79 sgk đại số 10
Chứng minh rằng:
\({x^3} + {\rm{ }}{y^3} \ge {\rm{ }}{x^2}y{\rm{ }} + {\rm{ }}x{y^2}\), \(∀x ≥ 0, ∀y ≥ 0\).
Giải
Ta có: \((x - y)^2\ge 0\Leftrightarrow {x^2} + {\rm{ }}{y^2}-{\rm{ }}2xy{\rm{ }} \ge {\rm{ }}0\)
\(\Leftrightarrow {x^2} + {\rm{ }}{y^2}-{\rm{ }}xy{\rm{ }} \ge xy\)
Do \(x ≥ 0, y ≥ 0\)
\(\Rightarrow x + y ≥ 0\),
Ta có
\(\left( {x{\rm{ }} + {\rm{ }}y} \right)({x^2} + {\rm{ }}{y^2}-{\rm{ }}xy){\rm{ }} \ge \left( {x{\rm{ }} + {\rm{ }}y} \right)xy\)
\(\Leftrightarrow {x^3} + {\rm{ }}{y^3} \ge {\rm{ }}{x^2}y{\rm{ }} + {\rm{ }}x{y^2}\)
Bài 5 trang 79 sgk đại số 10
Chứng minh rằng
\(x^4- \sqrt {{x^5}} + x - \sqrt x + 1 > 0, ∀x ≥ 0\).
Giải
Đặt \(\sqrt x = t, x ≥ 0 \Rightarrow t ≥ 0\).
Vế trái trở thành: \({t^8} - {t^5} + {t^2} - t + 1 = f(t)\)
+) Nếu \(t = 0\), hoặc \(t = 1\) thì \(f(t) = 1 >0\)
+) Với \(0 < t <1\),
\(f\left( t \right){\rm{ }} = {t^8} + {\rm{ }}({t^2} - {\rm{ }}{t^5}) + 1{\rm{ }} - {\rm{ }}t\)
\({t^8} > {\rm{ }}0;1{\rm{ }} - {\rm{ }}t{\rm{ }} > {\rm{ }}0,;{t^2} - {\rm{ }}{t^{5}} = {t^3}\left( {1{\rm{ }}-{\rm{ }}t} \right){\rm{ }} > {\rm{ }}0\).
Suy ra \(f(t) > 0\).
+) Với \(t > 1\) thì \(f\left( t \right){\rm{ }} = {t^5}({t^3}-{\rm{ }}1){\rm{ }} + {\rm{ }}t\left( {t{\rm{ }} - {\rm{ }}1} \right){\rm{ }} + {\rm{ }}1{\rm{ }} > {\rm{ }}0\)
Vậy \(f(t) > 0 ∀t ≥ 0\).
Hay \(x^4- \sqrt {{x^5}} + x - \sqrt x + 1 > 0, ∀x ≥ 0\).
Bài 6 trang 79 sgk đại số 10
Trong mặt phẳng tọa độ \(Oxy\), trên các tia \(Ox, Oy\) lần lượt lấy các điểm \(A\) và \(B\) thay đổi sao cho đường thẳng \(AB\) luôn tiếp xúc với đường tròn tâm \(O\) bán kính \(1\). Xác định tọa độ của \(A\) và \(B\) để đoạn \(AB\) có độ dài nhỏ nhất.
Giải
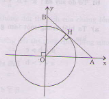
Ta có: \(2S_{OAB} = AB.OH = AB\) (vì \(OH = 1\)).
Vậy diện tích \(∆OAB\) nhỏ nhất khi \(AB\) có độ dài ngắn nhất.
Vì \(AB = AH + HB\) mà \(AH.HB = OH^2= 1\) nên \(AB\) có giá trị nhỏ nhất khi \(AH = HB\) tức \(∆OAB\) vuông cân: \(OA = OB\) và
\(AB = 2AH = 2OH = 2\).
\(AB^2= 4 = 2OA^2= 2OH = OA = OB = \sqrt2\).
Khi đó tọa độ của \(A, B\) là \(A(\sqrt 2; 0)\) và \(B(0; \sqrt2)\).
Giaibaitap.me
Giải bài tập trang 88 bài 2 Bất phương trình và hệ bất phương trình một ẩn Sách giáo khoa (SGK) Toán 10. Câu 1: Tìm các giá trị x thỏa mãn điều kiện của mỗi bất phương trình sau...
Giải bài tập trang 94 bài 3 Dấu của nhị thức bậc nhất Sách giáo khoa (SGK) Toán 10. Câu 1: Xét dấu các biểu thức...
Giải bài tập trang 99 bài 4 Bất phương trình bậc nhất hai ẩn Sách giáo khoa (SGK) Toán 10. Câu 1: Tập nghiệm của bất phương trình là...
Giải bài tập trang 105 bài 5 Dấu của tam thức bậc hai Sách giáo khoa (SGK) Toán 10. Câu 1: Xét dấu các tam thức bậc hai...
