Bài 1 trang 105 SGK Đại số 10

Xét dấu các tam thức bậc hai

a) ${x^{2}}-3x + 1$;                                                                

b) $- 2{x^2} + 3x + 5$;

c) ${x^2} +12x+36$;                                                            

d) $(2x - 3)(x + 5)$.

Giải

a) ${x^{2}}-3x + 1$

$∆ = (- 3)^2– 4.5 < 0  \Rightarrow   5x^2- 3x + 1 > 0  , ∀x ∈\mathbb R$ (vì luôn cùng dấu với $a=5 > 0$).

b) $- 2{x^2} + 3x + 5$

$- 2{x^2} + 3x + 5=0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr x = {5 \over 2} \hfill \cr} \right.$

  $- 2{x^2} + 3x + 5 <0$  với  $x \notin \left [ -1;\frac{5}{2} \right ]$

   $- 2{x^2} + 3x + 5 >0$ với   $- 1 < x < \frac{5}{2}$.

c) ${x^2} +12x+36$

$\Delta ' = {6^2} - 1.36 = 0$

${x^2} + 12x + 36 = 0 \Leftrightarrow x =  - 6$

Do đó: ${x^2} + 12x + 36 > 0, ∀x ≠ - 6$.

d) $(2x - 3)(x + 5)=2x^2+7x-15$

$(2x - 3)(x + 5) = 0 \Leftrightarrow \left[ \matrix{ x = - 5 \hfill \cr x = {3 \over 2} \hfill \cr} \right.$

Hệ số của tam thức là: $a=2 > 0$. Do đó: 

$(2x - 3)(x + 5) > 0$ với $x \notin \left[-5;\frac{3}{2}\right]$

$(2x - 3)(x + 5) < 0$ với $x \notin \left(-5;\frac{3}{2}\right).$

Bài 2 trang 105 SGK Đại số 10

Lập bảng xét dấu các biểu thức sau

a) $f(x) =(3{x^2} - 10x + 3)(4x - 5)$;

b) $f(x) = (3{x^2} - 4x)(2{x^2} - x - 1)$;

c) $f(x) = (4{x^2} - 1)( - 8{x^2} + x - 3)(2x + 9)$;

d) $f(x) = \frac{(3x^{2}-x)(3-x^{2})}{4x^{2}+x-3}.$

Giải

a) $f(x) =(3{x^2} - 10x + 3)(4x - 5)$ 

$3{x^2} - 10x + 3 = 0 \Leftrightarrow \left[ \matrix{ x = {1 \over 3} \hfill \cr x = 3 \hfill \cr} \right.$

$4x - 5 = 0 \Leftrightarrow x = {5 \over 4}$

    Bảng xét dấu:

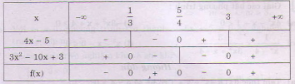
    Kết luận:

$f(x) < 0$ với $x \in \left( { - \infty ;{1 \over 3}} \right) \cup \left( {{5 \over 4};3} \right)$

$f(x) > 0$ với $x \in \left( {{1 \over 3};{5 \over 4}} \right) \cup \left( {3; + \infty } \right)$

b) $f(x) = (3{x^2} - 4x)(2{x^2} - x - 1)=0$

$\Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = {4 \over 3} \hfill \cr x = 1 \hfill \cr x = - {1 \over 2} \hfill \cr} \right.$

Bảng xét dấu:

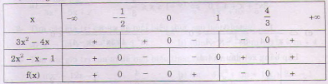
c) $f(x) = (4{x^2} - 1)( - 8{x^2} + x - 3)(2x + 9)=0$

$\Leftrightarrow \left[ \matrix{ x = {1 \over 2} \hfill \cr x = - {1 \over 2} \hfill \cr x = - {9 \over 2} \hfill \cr} \right.$

Bảng xét dấu:

d) $f(x) = \frac{(3x^{2}-x)(3-x^{2})}{4x^{2}+x-3}=0$

$\Leftrightarrow \left[ \matrix{ x = \sqrt 3 \hfill \cr x = - \sqrt 3 \hfill \cr x = {1 \over 3} \hfill \cr x = 0 \hfill \cr} \right.$

    Bảng xét dấu:

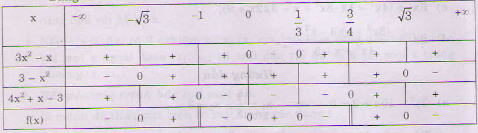
Bài 3 trang 105 SGK Đại số 10

Giải các bất phương trình sau

a) $4{x^2} - x + 1 < 0$;                                                      

b) $- 3{x^2} + x + 4 \ge 0$;

c) $\frac{1}{x^{2}-4}<\frac{3}{3x^{2}+x-4};$                                 

d) $x^2- x - 6 ≤ 0$. 

Hướng dẫn.

a) Tam thức $f(x) =4{x^2} - x + 1 < 0$ có hệ số $a = 4 > 0$ biệt thức $∆ = (-1)^2- 4.4.1 < 0$. Do đó $f(x) > 0 ,∀x ∈\mathbb R$. 

Bất phương trình $4{x^2} - x + 1 < 0$ vô nghiệm.

b) $- 3{x^2} + x + 4 \ge 0$

$f(x) = - 3{x^2} + x + 4 = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr x = {4 \over 3} \hfill \cr} \right.$

Do đó: $- 3{x^2} + x + 4 \ge 0 \Leftrightarrow  - 1 \le x \le {4 \over 3}$

c) $\frac{1}{x^{2}-4}<\frac{3}{3x^{2}+x-4}$  

   $\Leftrightarrow \frac{1}{x^{2}-4}-\frac{3}{3x^{2}+x-4}< 0$

   $\Leftrightarrow \frac{x+8}{(x^{2}-4)(3x^{2}+x-4)}< 0$

    Lập bảng xét dấu vế trái: 

    Tập nghiệm của bất phương trình $S = (-∞; - 8) ∪ \left(- 2; -\frac{4}{3}\right) ∪ (1; 2)$.

d) $x^2- x - 6 ≤ 0$

$x^2- x - 6 =0$ $\Leftrightarrow \left[ \matrix{ x = 3 \hfill \cr x = - 2 \hfill \cr} \right.$

Tập nghiệm của bất phương trình là: $S =[- 2; 3]$.

Bài 4 trang 105 sgk đại số 10

Tìm các giá trị của tham số $m$ để các phương trình sau vô nghiệm

a) $(m - 2)x^2+ 2(2m – 3)x + 5m – 6 = 0$; 

b) $(3 - m)x^2- 2(m + 3)x + m + 2 = 0$.

Giải

a) +) Với $m = 2$ phương trình trở thành $2x + 4 = 0$ có $1$ nghiệm, do đó trường hợp này không thỏa mãn.

    +) Với $m\ne 2$

   Phương trình vô nghiệm nếu:

    $\left\{\begin{matrix} m-2\neq 0\\ \Delta ^{'}=(2m-3)^{2}-(m-2)(5m-6)< 0 \end{matrix}\right.$

    $\Leftrightarrow$ $\left\{\begin{matrix} m-2\neq 0\\ -m^{2}+4m-3< 0 \end{matrix}\right.$ 

   $\Leftrightarrow m < 1 ∪ m > 3$.

b) +) Với $m = 3$, phương trình trở thành: $- 6x + 5 = 0$ có nghiệm. Loại trường hợp $m = 3$.

    +) Với $m\ne 3$

    Phương trình vô nghiệm khi và chỉ khi:

$\eqalign{ & \Leftrightarrow \left\{ \matrix{ m \ne 3 \hfill \cr \Delta ' = {(m + 3)^2} - (3 - m).(m + 2) < 0 \hfill \cr} \right. \cr & \Leftrightarrow \left\{ \matrix{ m \ne 3 \hfill \cr 2{m^2} + 5m + 3 < 0 \hfill \cr} \right. \Leftrightarrow - {3 \over 2} < m < - 1 \cr & \cr}$

 Giaibaitap.me