Bài 1 trang 94 SGK Đại số 10

 Xét dấu các biểu thức: 

a) \(f(x) = (2x - 1)(x + 3)\);                        

b) \(f(x) = (- 3x - 3)(x + 2)(x + 3)\);

c)\( f(x) = \frac{-4}{3x+1}-\frac{3}{2-x};\)               

d) \(f(x) = 4x^2– 1\).

Giải

a) Ta lập bảng xét dấu

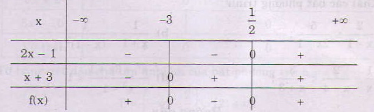
Kết luận: \(f(x) < 0\) nếu \(- 3 < x < \frac{1}{2}\)

              \(f(x) = 0\) nếu \(x = - 3\) hoặc \(x = \frac{1}{2}\)

              \(f(x) > 0\) nếu \(x < - 3\) hoặc \(x > \frac{1}{2}\).

b) Ta lập bảng xét dấu 

              \( f(x) < 0\) nếu \(x ∈ (- 3; - 2) ∪ (- 1; +∞)\)

               \(f(x) = 0\) với \(x = - 3\), \(x= - 2\), hoặc \(x= - 1\)

               \(   f(x) > 0\) với \(x ∈ (-∞; - 3) ∪ (- 2; - 1)\).

c) Ta có: \(f(x) = \frac{-4}{3x+1}-\frac{3}{2-x}=\frac{5x+11}{(3x+1)(x-2)}\)

Ta lập bảng xét dấu

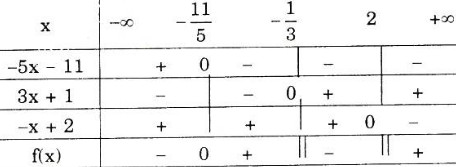
             \(f(x)\) không xác định nếu \(x = -\frac{1}{3}\) hoặc \(x = 2\)

             \(f(x) < 0\) với \(x ∈ \left ( -\infty ;-\frac{11}{5} \right )\) ∪ \(\left ( -\frac{1}{3};2 \right )\)

             \(f(x) > 0\) với \(x ∈ \left ( -\frac{11}{5};-\frac{1}{3} \right )∪ (2; +∞)\).

d) \(f(x) = 4x^2– 1 = (2x - 1)(2x + 1)\).

Ta lập bảng xét dấu

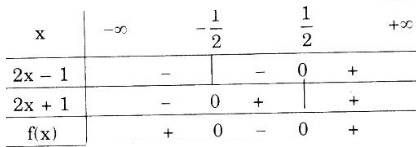
             \(f(x) = 0\) với \(x = \pm \frac{1}{2}\)

             \(f(x) < 0\) với \(x ∈ \left ( -\frac{1}{2};\frac{1}{2} \right )\)

             \(f(x) > 0\) với \(x ∈ \left ( -\infty ;-\frac{1}{2} \right )∪ \left ( \frac{1}{2};+\infty \right ).\) 

Bài 2 trang 94 sgk đại số 10

Giải các bất phương trình

a) \(\frac{2}{x-1}\leq \frac{5}{2x-1};\)                                       

b) \(\frac{1}{x+1}<\frac{1}{(x-1)^{2}};\)

c) \(\frac{1}{x}+\frac{2}{x+4}<\frac{3}{x+3};\)                                 

d) \(\frac{x^{2}-3x+1}{x^{2}-1}<1.\)

Giải

a) \(\frac{2}{x-1}\leq \frac{5}{2x-1}\) 

 \(\Leftrightarrow f(x) = -\frac{5}{2x-1}+\frac{2}{x-1}=\frac{-x+3}{(2x-1)(x-1)}\leq 0\).

Xét dấu của \(f(x)\) ta được bảng xét dấu:

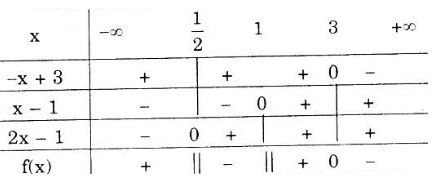
Tập nghiệm của bất phương trình là: 

                                \(T = \left ( \frac{1}{2};1 \right ) ∪ [3; +∞)\).

b) \(\frac{1}{x+1}<\frac{1}{(x-1)^{2}}\) 

\( \Leftrightarrow  f(x) = \frac{1}{x+1}-\frac{1}{(x-1)^{2}} = \frac{x(x-3)}{(x+1)(x-1)^{2}}< 0\).

\(f(x)\) không xác định với \(x = ± 1\). 

Xét dấu của \(f(x)\) ta được bảng xét dấu:

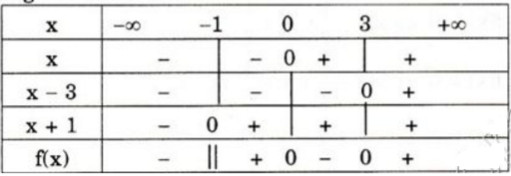
Tập nghiệm của bất phương trình là:

                      \(T = (-∞; - 1) ∪ (0; 1) ∪ (1; 3)\).

c) \(\frac{1}{x}+\frac{2}{x+4}<\frac{3}{x+3} \Leftrightarrow  f(x) = \frac{1}{x}+\frac{2}{x+4}-\frac{3}{x+3}\) 

\(= \frac{x+12}{x(x+3)(x+4)} < 0\).

Bảng xét dấu:

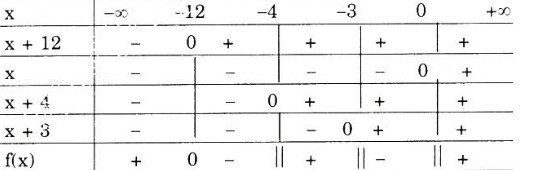
Tập nghiệm của bất phương trình là: \(T = \left ( -12;-4 \right ) ∪ (-3; 0)\).

 d) \(\frac{x^{2}-3x+1}{x^{2}-1}<1\)

\( \Leftrightarrow f(x) = {{{x^2} - 3x + 1} \over {{x^2} - 1}} - 1 = {{{x^2} - 3x + 1 - {x^2} + 1} \over {{x^2} - 1}} = {{ - 3x + 2} \over {(x - 1)(x + 1)}} < 0\)

Bảng xét dấu:

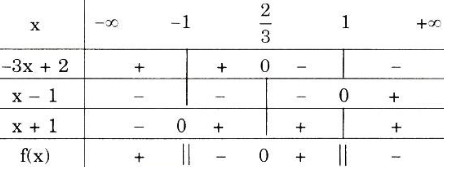
Tập nghiệm của bất phương trình là: \(T = \left ( -1;\frac{2}{3} \right ) ∪ (1; +∞)\).

Bài 3 trang 94 sgk đại số 10

Giải các bất phương trình

a) \(|5x - 4| ≥ 6\);                                                

b) \(\left | \frac{-5}{x+2} \right |<\left | \frac{10}{x-1} \right |.\)

Giải

a) \(|5x - 4| ≥ 6\)

\(\eqalign{
& \Leftrightarrow {(5x - 4)^2} \ge {6^2} \Leftrightarrow {(5x - 4)^2} - {6^2} \ge 0 \cr
& \Leftrightarrow (5x - 4 - 6)(5x - 4 + 6) \ge 0 \cr
& \Leftrightarrow (5x - 10)(5x + 2) \ge 0 \cr} \)

Bảng xét dấu:

Từ bảng xét dấu cho tập nghiệm của bất phương trình:

                              \(T =\left( { - \infty ; - {2 \over 5}} \right] ∪ [2; +∞)\).

b) \(\left | \frac{-5}{x+2} \right |<\left |\frac{10}{x-1} \right |\)

\(\eqalign{
& \Leftrightarrow {5 \over {|x + 2|}} < {{10} \over {|x - 1|}} \Leftrightarrow {1 \over {|x + 2|}} < {2 \over {|x - 1|}} \cr
& \Leftrightarrow 2|x + 2| - |x - 1| > 0  \text{     } (1)\cr} \)  

Bảng xét dấu:

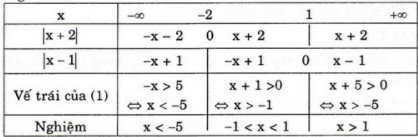
Tập nghiệm của bất phương trình là: \(T = (-∞; - 5) ∪ (- 1; 1) ∪ (1; +∞)\).

Giaibaitap.me