Bài 4 sgk trang 40 hình học 10
Chứng minh rằng với mọi góc \(α (0^0≤ α ≤ 180^0)\) ta đều có \(si{n^2}\alpha + {\cos ^2}\alpha = 1\)
Giải
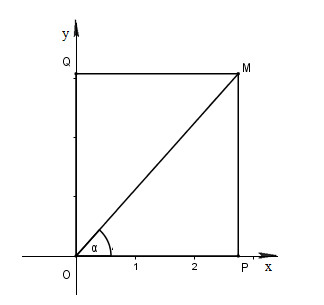
Từ \(M\) kẻ \(MP ⊥ Ox\), \(MQ ⊥ Oy\)
Xét tam giác vuông \(AMP\) có:
\(sin\alpha = {{MP} \over {OM}};\cos \alpha = {{OP} \over {OM}} \)
\(\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = {{M{P^2} + O{P^2}} \over {O{M^2}}} = {{O{M^2}} \over {O{M^2}}} = 1\)
Bài 5 sgk trang 40 hình học 10
Cho góc \(x\), với \(\cos x = \frac{1}{3}\)
Tính giá trị của biểu thức: \( P = 3\sin^2x +\cos^2x\).
Giải:
Ta có
\(\eqalign{
& {\sin ^2}x + {\cos ^2}x = 1 \cr
& \Rightarrow {\sin ^2}x = 1 - {\cos ^2}x \cr} \)
Do đó \(P = 3{\sin ^2}x + {\cos ^2}x = 3(1 - {\cos ^2}x) + {\cos ^2}x \)
\(= 3 - 2{\cos ^2}x = 3 - 2.{\left( {{1 \over 3}} \right)^2} = {{25} \over 9}\)
Bài 6 sgk trang 40 hình học 10
Cho hình vuông \(ABCD\),
Tính: \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right),sin\left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right),\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right)\)
Giải
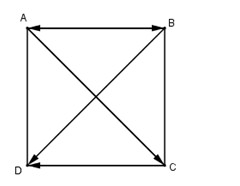
Ta có :
$$\eqalign{
& \cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right) = \cos {135^0} = {{\sqrt 2 } \over 2}, \cr
& sin\left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right) = \sin {90^0} = 1, \cr
& \cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \cos {0^0} = 1 .\cr} $$
Giaibaitap.me
Giải bài tập trang 45 bài 2 Tích vô hướng của hai vectơ Sách giáo khoa (SGK) Hình học 10. Câu 1: Cho tam giác vuông cân ...
Giải bài tập trang 45 bài 2 Tích vô hướng của hai vectơ Sách giáo khoa (SGK) Hình học 10. Câu 5: Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ ...
Giải bài tập trang 59 bài 3 Các hệ thức lượng trong tam giác và giải tam giác Sách giáo khoa (SGK) Hình học 10. Câu 1: Cho tam giác ...
Giải bài tập trang 59 bài 3 Các hệ thức lượng trong tam giác và giải tam giác Sách giáo khoa (SGK) Hình học 10. Câu 5: Tính cạnh BC ...
