Bài 1 trang 45 sgk hình học 10

Cho tam giác vuông cân \(ABC\) có \(AB = AC = a\). Tính các tích vô hướng \(\vec{AB}.\vec{AC}\), \(\vec{AC}.\vec{CB}\).

Giải

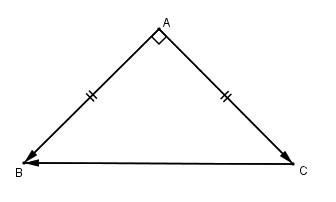
\(\vec{AB} ⊥\vec{AC}\Rightarrow \vec{AB}.\vec{AC}  = 0\)

\(\vec{AC}.\vec{CB} =- \vec{CA}\). \(\vec{CB}\)

Ta có: \(CB= a\sqrt2\);  \(\widehat{C} = 45^0\) 

Vậy   \(\vec{AC}.\vec{CB} = -\vec{CA}. \vec{CB}= -|\vec{CA}|. |\vec{CB}|. cos45^0\)

\(= - a.a\sqrt 2 .{{\sqrt 2 } \over 2} =  - {a^2}\)

Bài 2 trang 45 sgk hình học 10

Cho ba điểm \(O, A, B\) thẳng hàng biết \(OA = a, OB = b\). tính tích vô hướng của \(\vec{OA}\).\(\vec{OB}\) trong \(2\) trường hợp

a) Điểm \(O\) nằm ngoài đoạn \(AB\)

b) Điểm \(O\) nằm trong đoạn \(AB\)

Giải

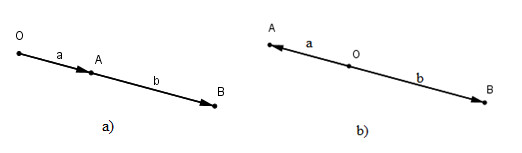
a) Khi \(O\) nằm ngoài đoạn \(AB\) thì  hai vec tơ \(\vec{OA}\) và \(\vec{OB}\) cùng hướng và góc

\((\vec{OA}, \vec{OB}) = 0^0\)

     \(\cos(\vec{OA}, \vec{OB}) = 1\)   nên  \(\vec{OA}.\vec{OB} = a.b\)

b)  Khi \(O\) nằm ngoài trong đoạn \(AB\) thì  hai vectơ \(\vec{OA}\) và \(\vec{OB}\) ngược hướng và góc

(\(\vec{OA}, \vec{OB}) = 180^0\) 

       \(\cos(\vec{OA}, \vec{OB}) = -1\)   nên  \(\vec{OA}.\vec{OB} = -a.b\)

Bài 3 trang 45 sgk hình học 10

Cho nửa đường tròn tâm \(O\) có  đường kính \(AB = 2R\). Gọi \(M\) và \(N\) là hai điểm thuộc nửa đường tròn sao cho hai dây cung \(AM\) và \(BN\) cắt nhau tại \(I\).

a) Chứng minh \(\overrightarrow {AI} .\overrightarrow {AM}  = \overrightarrow {AI} .\overrightarrow {AB}\) và \(\overrightarrow {BI} .\overrightarrow {BN}  = \overrightarrow {BI} .\overrightarrow {BA}\);

B) Hãy dùng câu a) để tính \(\overrightarrow {AI} .\overrightarrow {AM}  + \overrightarrow {BI} .\overrightarrow {BN}\) theo \(R\)

Giải

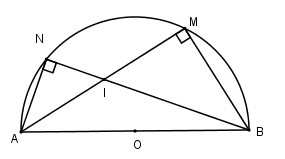
Ta có :  \(\left( {\overrightarrow {AI} .\overrightarrow {AB} } \right) = \overrightarrow {AI} \left( {\overrightarrow {AM}  + \overrightarrow {MB} } \right) = \overrightarrow {AI} .\overrightarrow {AM}  + \overrightarrow {AI} .\overrightarrow {MB} \)

Mặt khác: \(\overrightarrow {AI}  \bot \overrightarrow {MB} \) nên \(\overrightarrow {AI} .\overrightarrow {MB}  = 0\) 

Từ đó: \(\overrightarrow {AI} .\overrightarrow {AM}  = \overrightarrow {AI} .\overrightarrow {AB} \)

Ta có: \(\overrightarrow {BI} .\overrightarrow {BA}  = \overrightarrow {BI} \left( {\overrightarrow {BN}  + \overrightarrow {NA} } \right) = \overrightarrow {BI} .\overrightarrow {BN}  + \overrightarrow {BI} .\overrightarrow {NA} \)

Mặt khác: \(\overrightarrow {BI}  \bot \overrightarrow {NA} \) nên \(\overrightarrow {BI} .\overrightarrow {NA}  = 0\)  

Từ đó: \(\overrightarrow {BI} .\overrightarrow {BN}  = \overrightarrow {BI} .\overrightarrow {BA} \)

b)  

\(\eqalign{
& \overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\overrightarrow {BA} \cr
& = \overrightarrow {AI} .\overrightarrow {AB} - \overrightarrow {BI} .\overrightarrow {AB} = \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right) \cr
& = \overrightarrow {AB} .\overrightarrow {AB} = {\overrightarrow {AB} ^2} = 4{{\rm{R}}^2} \cr} \)

Bài 4 trang 45 sgk hình học 10

 Trên mặt phẳng \(Oxy\), cho hai điểm \(A(1; 3), B(4;2)\)

a) Tìm tọa độ điểm \(D\) nằm trên trục \(Ox\) sao cho \(DA = DB\);

b) Tính chu vi tam giác \(OAB\);

c) Chứng tỏ rằng \(OA\) vuông góc với \(AB\) và từ đó tính diện tích tam giác \(OAB\)

Giải

a) \(D\) nằm trên trục \(Ox\) nên tọa độ của \(D\) là \((x; 0)\).

 Ta có : 

\(\eqalign{
& DA = DB \cr
& \Leftrightarrow D{A^2} = D{B^2} \cr
& \Leftrightarrow {(1 - x)^2} + {3^2} = {(4 - x)^2} + {2^2} \cr
& \Leftrightarrow 1 - 2x + {x^2} + 9 = 16 - 8x + {x^2} + 4 \cr
& \Leftrightarrow 6x = 10 \cr
& \Leftrightarrow x = {5 \over 3} \cr
& \Rightarrow D\left( {{5 \over 3};0} \right) \cr} \)

b) 

\(\eqalign{
& O{A^2} = {1^2} + {3^3} = 10 \Rightarrow OA = \sqrt {10} \cr
& O{B^2} = {4^2} + {2^2} = 20 \Rightarrow OB = 2\sqrt 5 \cr
& A{B^2} = {(4 - 1)^2} + {(2 - 3)^2} = 10 \Rightarrow AB = \sqrt {10} \cr} \)

Chu vi tam giác \(OAB\) là: \(\sqrt {10}  + 2\sqrt 5  + \sqrt {10} \)

c) Ta có \(\vec{OA}= (1; 3)\)

            \(\vec{AB} = (3; -1)\)

\(\vec{OA} .\vec{AB} = 1.3 + 3.(-1) = 0 \Rightarrow \vec{OA}\) ⊥ \(\vec{AB}\) 

\({S_{OAB}}=\frac{1}{2}|\vec{OA}| .|\vec{AB}| =5\) (đvdt)

Giaibaitap.me