Bài 1 trang 59 sgk hình học 10
Cho tam giác \(ABC\) vuông tại \(A\), \(\widehat{B}= 58^0\)
và cạnh \(a = 72 cm\). Tính \(\widehat{C}\), cạnh \(b\), cạnh \(c\) và đường cao \(h_a\)
Giải
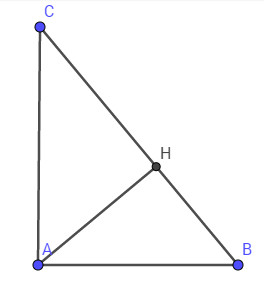
Theo định lí tổng \(3\) góc trong một tam giác ta có:
\(\eqalign{
& \widehat A + \widehat B + \widehat C = {180^0} \cr
& \Rightarrow \widehat C = {180^0} - \widehat A - \widehat B = {180^0} - {90^0} - {58^0} = {32^0} \cr} \)
Xét tam giác vuông \(ABC\) có:
\(b = a.\cos {32^0} \Rightarrow b \approx 61,06cm\);
\(c = a.sin{32^0} \Rightarrow c \approx 38,15cm\)
\(h_a =\frac{b.c}{a}\) \(\Rightarrow h_a ≈ 32,36cm\)
Bài 2 trang 59 sgk hình học 10
Cho tam giác \(ABC\) biết các cạnh \(a = 52, 1cm\); \(b = 85cm\) và \(c = 54cm\). Tính các góc \(\widehat{A}\), \(\widehat{B}\), \(\widehat{C}\).
Giải
Từ định lí cosin
\({a^2} = {b^2} + {c^2} - 2bc.cosA\)
ta suy ra \(\cos A = \frac{b^{2}+c^{2}-a^{2}}{2bc}\) = \(\frac{85^{2}+54^{2}-(52,1)^{2}}{2.85.54}\)
\(\Rightarrow \cos A ≈ 0,8089 \Rightarrow \widehat{A}= 36^0\)
Tương tự, ta tính được \(\widehat{B}≈ 106^028’\) ;
\(\widehat{C}≈ 37^032’\).
Bài 3 trang 59 sgk hình học 10
Cho tam giác \(ABC\) có \(\widehat{A} = 120^0\) cạnh \(b = 8cm\) và \(c = 5cm\). Tính cạnh \(a\), và góc \(\widehat{B}\), \(\widehat{C}\) của tam giác đó.
Giải
Ta có
\(\eqalign{
& {a^2} = {8^2} + {5^2} - 2.8.5.cos{120^0} = 64 + 25 + 40 = 129 \cr
& \Rightarrow a = \sqrt {129} \approx 11,36cm \cr} \)
Ta có thể tính góc \(B\) theo định lí cosin
\(\cos B = \frac{a^{2}+c^{2}-b^{2}}{2ac} = \frac{129 + 25 - 64}{2.\sqrt{129}.5} ≈ 0,7936 \)
\(\Rightarrow\widehat{B}= 37^048’\)
Ta cũng có thể tính góc \(B\) theo định lí sin :
\(\cos B = \frac{11,36}{\sin120^{0}}= \frac{8}{\sin B}\) \(\Rightarrow \sin B ≈ 0,6085\)
\(\Rightarrow\widehat{B}= 37^048’\)
Tổng ba góc trong một tam giác bằng \(180^0\)
\(\widehat{C}=180^0- (\widehat{A} + \widehat{B})\)
\(\Rightarrow\widehat{C}= 22^012’\).
Bài 4 trang 59 sgk hình học 10
Tính diện tích \(S\) của tam giác có số đo các cạnh lần lượt là \(7, 9\) và \(12\).
Giải
Ta có \(2p = 7 + 9 + 12 \Rightarrow p = 14\)
\(p - a = 14 - 7 = 7\)
\(p - b = 14 - 9 = 5\)
\(p - c = 12 - 12 = 2\)
Áp dụng công thức Hêrong:
\(S = \sqrt{14.7.5.2} = \sqrt{2^{2}.7^{2}.5} = 14\sqrt 5\approx 31,3\) (dvdt)
Giaibaitap.me
Giải bài tập trang 59 bài 3 Các hệ thức lượng trong tam giác và giải tam giác Sách giáo khoa (SGK) Hình học 10. Câu 5: Tính cạnh BC ...
Giải bài tập trang 59, 60 bài 3 Các hệ thức lượng trong tam giác và giải tam giác Sách giáo khoa (SGK) Hình học 10. Câu 9: Cho hình bình hành...
Giải bài tập trang 62 bài ôn tập chương II - tích vô hướng của hai vectơ và ứng dụng Sách giáo khoa (SGK) Hình học 10. Câu 1: Hãy nhắc lại định nghĩa giá trị lượng giác của một góc...
Giải bài tập trang 62 bài ôn tập chương II - tích vô hướng của hai vectơ và ứng dụng Sách giáo khoa (SGK) Hình học 10. Câu 5: Hãy nhắc lại định lí cosin trong tam giác. ..
