Câu 26 trang 66 SGK Hình học 10

Tam giác \(ABC\) có \(A = (10; 5), B = (3; 2), C = (6; -5)\). Khẳng định nào sau đây là đúng?

A. \(ABC\) là tam giác đều

B. \(ABC\) là tam giác vuông cân tại \(B\)

C. \(ABC\) là tam giác vuông cân tại \(A\)

D. \(ABC\) là tam giác có góc tù tại \(A\).

Trả lời:

Chọn B.

$$\eqalign{
& AB = \sqrt {{{(3 - 10)}^2} + {{(2 - 5)}^2}} = \sqrt {58} \cr
& BC = \sqrt {{{(6 - 10)}^2} + {{( - 5 - 5)}^2}} = \sqrt {58} \cr
& BC = \sqrt {{{(6 - 3)}^2} + {{( - 5 - 2)}^2}} = \sqrt {116} \cr} $$

Câu 27 trang 66 SGK Hình học 10

Tam giác \(ABC\) vuông cân tại \(A\) và nội tiếp trong đường tròn tâm \(O\) bán kính \(R\). Gọi \(R\) là bán kính đường tròn nội tiếp tam giác \(ABC\). Khi đó tỉ số \({R \over r}\) là:

A. \(1 + \sqrt 2\)                                                  

B. \({{2 + \sqrt 2 } \over 2}\)

C. \({{\sqrt 2  - 1} \over 2}\)                                                   

D. \({{1 + \sqrt 2 } \over 2}\)

Trả lời:

Ta có:

\(\left. \matrix{
{S_{ABC}} = {R^2} \hfill \cr
p = {1 \over 2}(R\sqrt 2 + R\sqrt 2 + 2R) \hfill \cr} \right\} \Rightarrow p = R(\sqrt 2 + 1)\)

Suy ra: \(r = {S \over p} = {R \over {\sqrt 2  + 1}} \Rightarrow {R \over r} = \sqrt 2  + 1\)

Vậy chọn A.

Câu 28 trang 66 SGK Hình học 10

Tam giác \(ABC\) có \(AB = 9cm, AC = 12cm, BC = 15cm\). Khi đó đường trung tuyến \(AM\) của tam giác có độ dài là:

A. \(8cm\)                             B. \(10cm\)    

C. \(9cm\)                             D. \(7,5cm\)

Trả lời:

Áp dụng công thức: \({m_a}^2 = {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4}\)

\(\eqalign{
& A{M^2} = {{{{12}^2} + {9^2}} \over 2} - {{{{15}^2}} \over 4} = 56,25 \cr
& \Leftrightarrow AM = \sqrt {56,25} = 7,5cm \cr} \)

Chọn D

Câu 29 trang 67 SGK Hình học 10

 Tam giác \(ABC\) có \(BC = a, CA = b, AB  = c\) và có diện tích \(S\). Nếu tăng cạnh \(BC\) lên \(2\) lần đồng thời tăng cạnh \(CA\) lên \(3\) lần và giữ nguyên độ lớn của góc \(C\) thì khi đó diện tích tam giác mới được tạo nên bằng:

A. \(2S\)                 B. \(3S\)

C. \(4S\)                     D. \(6S\).

Trả lời:

Áp dụng công thức:

\(\left. \matrix{
S = {1 \over 2}ab\sin C \hfill \cr
S' = {1 \over 2}(2a.3b)\sin C \hfill \cr} \right\} \Rightarrow {{S'} \over S} = 6 \Rightarrow S' = 6S\)

 Vậy chọn D

Bài 30. Cho tam giác \(DEF\) có \(DE = DF =10cm\) và \(EF = 12cm\). Gọi \(I\) là trung điểm của cạnh \(EF\). Đoạn thẳng \(DI\) có độ dài là:

A. \(6,5 cm\)                                      B. \(7cm\)

C. \(8cm\)                                          D. \(4cm\)

Trả lời:

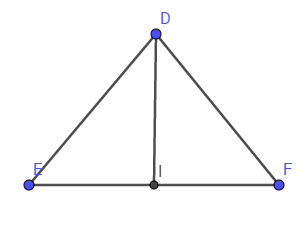
Ta có: \(DI\) là đường trung tuyến của tam giác \(DEF\)

Áp dụng công thức tính độ dài đường trung tuyến: \({m_a}^2 = {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4}\)

\(\eqalign{
& D{I^2} = {{{{10}^2} + {{10}^2}} \over 2} - {{{{12}^2}} \over 4} = 64 \cr 
& \Rightarrow DI = \sqrt {64} = 8cm \cr} \)

Vậy chọn C.

Giaibaitap.me