Câu 23 trang 32 SGK Hình học 10

Cho \(\overrightarrow a  = ( - 1;2);\overrightarrow b  = (5; - 7)\) . Tọa độ của vecto \(\overrightarrow a  - \overrightarrow b \) là:

a) \((6; -9)\)                        b) \((4; -5)\)                            

c) \((-6; 9)\)                        d) \((-5; -14)\)

Trả lời:

\(\left\{ \matrix{
\overrightarrow a = ( - 1;2) \hfill \cr
\overrightarrow b = (5; - 7) \hfill \cr} \right. \Rightarrow \overrightarrow a - \overrightarrow b = ( - 6;9)\)

Chọn C

Câu 24 trang 32 SGK Hình học 10

Cho \(\overrightarrow a  = (5;0);\overrightarrow b  = (4;x)\) . Hai vectơ \(a\) và \(b\) cùng phương nếu số \(x\) là:

a) -5                     b) 4                      c) 0                                d) -1

Trả lời:

Ta có:

\(\eqalign{
& \left\{ \matrix{
\overrightarrow a = (5,0) \hfill \cr
\overrightarrow b = (4,x) \hfill \cr} \right. \Rightarrow \overrightarrow a //\overrightarrow b \Rightarrow \left\{ \matrix{
- 5 = 4k \hfill \cr
0 = kx \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
k = - {5 \over 4} \hfill \cr
x = 0 \hfill \cr} \right. \cr
& \Rightarrow x = 0 \cr} \)

Chọn C

Câu 25 trang 32 SGK Hình học 10

Cho \(\overrightarrow a  = (x;2);\overrightarrow b  = ( - 5;1);\overrightarrow c  = (x;7)\) . Vectơ \(\overrightarrow c  = 2\overrightarrow a  + 3\overrightarrow b \) nếu:

a) \(x = -15\)                            b) \(x = 3\)                        

c) \(x = 15\)                             d) \(x = 5\)

Trả lời:

Ta có: \(\overrightarrow a  = (x;2);\overrightarrow b  = ( - 5;1);\overrightarrow c  = (x;7)\) nên: 

\(\eqalign{
& \overrightarrow c = 2\overrightarrow a + 3\overrightarrow b = (2x - 15,7) \cr
& \Rightarrow \left\{ \matrix{
2x - 15 = x \hfill \cr
7 = 7 \hfill \cr} \right. \Leftrightarrow x = 15 \cr} \)

chọn C

Câu 26 trang 32 SGK Hình học 10

Cho \(A(1;1); B(-2; -2); C(7; 7)\). Khẳng định nào đúng?

A. \(G(2;2)\) là trọng tâm của tam giác \(ABC\)

B. Điểm \(B\) ở giữa hai điểm \(A\) và \(C\)

C. Điểm \(A\) ở giữa hai điểm \(B\) và \(C\)

D. Hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng.

Trả lời:

a) \(G(2; 2) ⇒\) A đúng4

c) Ta lại có:

\(\eqalign{
& \overrightarrow {AB} = ( - 3; - 3) = - 3(1;1) \cr
& \overrightarrow {AC} = (6;6) = 6(1;1) \Rightarrow \overrightarrow {AC} = - 2\overrightarrow {AB} \cr} \)

\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là hai vectơ ngược hướng, suy ra điểm \(A\) ở giữa hai điểm \(B\) và \(C\).

Do đó C sai.

B và D là khẳng định sai.

Vậy chọn A.

Câu 27 trang 32 SGK Hình học 10

Các điểm \(M(2; 3); N(0; -4); P(-1; 6)\) lần lượt là trung điểm các cạnh \(BC, CA, AB\) của tam giác \(ABC\). Tọa độ của đỉnh \(A\) là:

a) \((1; 5)\)                               b) \((-3; 1)\)                    

c) \((-2; -7)\)                            d) \((1; -10)\)

Trả lời:

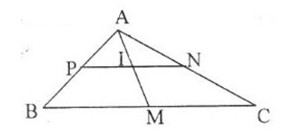
Trung tuyến \(AM\) cắt \(PN\) tại \(I\) thì \(I\) là trung điểm của \(PN\) nên \(I( - {1 \over 2},1)\) và \(I\) cũng là trung điểm của \(AM\).

Suy ra: \(A\) đối xứng với \(M\) qua \(I\) nên:

\(\left\{ \matrix{
{x_A} + {x_M} = 2{x_I} \hfill \cr
{y_A} + {y_M} = 2{y_I} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_A} = 2{x_I} - {x_M} = - 3 \hfill \cr
{y_A} = 2{y_I} - {y_M} = - 1 \hfill \cr} \right.\)

Vậy \(A(-3, -1) ⇒\) chọn B.

Giaibaitap.me