Câu 5 trang 106 SGK Đại số 10
Trên cùng một mặt phẳng tọa độ, hãy vẽ đồ thị hai hàm số:
y=f(x)=x+1 và y=g(x)=3−x
và chỉ ra các giá trị nào của x thỏa mãn
a) f(x)=g(x)
b) f(x)>g(x)
c) f(x)<g(x)
Kiểm tra lại kết quả bằng cách giải phương trình, bất phương trình.
Trả lời:
Đồ thị hàm số :
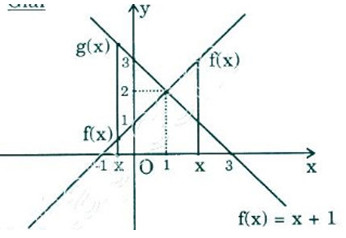
a) Đồ thị của y=f(x)=x+1 và y=g(x)=3−x cắt nhau tại điểm A(1;2)
Tại x=1 thì f(x)=g(x)=2
Kiểm tra bằng tính toán:
F(x)=g(x)⇔x+1=3−x⇔x=2
b) Khi x>1 thì đồ thị hàm số y=f(x) nằm phía trên đồ thị y=g(x).
Vậy với x>1 thì f(x)>g(x).
Kiểm tra lại bằng tính toán:
f(x)>g(x))⇔x+1>3−x⇔2x>2⇔x>1
c) Với x<1 thì đồ thị hàm số y=g(x) nằm phía trên dồ thị y=f(x)
Vậy với x<1 thì g(x)>f(x)
Kiểm tra lại bằng tính toán:
f(x)<g(x)⇔x+1<3−x⇔2x<2⇔x<1
Câu 6 trang 106 SGK Đại số 10
Cho a,b,c>0. Chứng minh rằng: a+bc+b+ca+c+ab≥6
Trả lời:
Vế trái bất đẳng thức có thể viết là:
a+bc+b+ca+c+ab
= (ac+ca)+(bc+cb)+(ba+ab)
Ta biết với a,b,c>0 áp dụng bất đẳng thức cô-si ta có:
(ac+ca)+(bc+cb)+(ba+ab)≥2.√ac.ca+2.√bc.cb+2.√ba.ab=2.1+2.1+2.1=6
Vậy a+bc+b+ca+c+ab≥6
Câu 7 trang 107 SGK Đại số 10
Điều kiện của một bất phương trình là gì? Thế nào là hai bất phương trình tương đương?
Trả lời:
+ Điều kiện của bất phương trình f(x).g(x) là các điều kiện của ẩn x sao cho các biểu thức f(x) và g(x) có nghĩa.
+ Hai bất phương trình là tương đương nếu chúng có cùng tập nghiệm.
+ Biến đổi một bất phương trình thành một bất phương trình có cùng tập nghiệm gọi là phép biến đổi tương đương.
Câu 8 trang 107 SGK Đại số 10
Nêu quy tắc giải bất phương trình ax+by≤c
Trả lời:
+ Ta vẽ đường thẳng (d):ax+by=c
+ Chọn điểm M(x0;y0)∉(d) (thường là điểm (0;0)) và tính giá trị ax0+by0
+ Nếu ax0+by0>c thì nửa mặt phẳng bờ (d) không chứa M(x0;y0) là tập hợp các điểm mà tọa độ của nó là nghiệm của bất phương trình.
+ Nếu ax0+by0<c thì nửa mặt phẳng bờ (d) chứa M(x0;y0) là tập hợp các điểm có tọa độ là nghiệm của bất phương trình.
Giaibaitap.me
Giải bài tập trang 106 bài ôn tập chương IV - bất đẳng thức, bất phương trình Sách giáo khoa (SGK) Toán 10. Câu 9: Phát biểu định lí về dấu của tam thức bậc hai...
Giải bài tập trang 107 bài ôn tập chương IV - bất đẳng thức, bất phương trình Sách giáo khoa (SGK) Toán 10. Câu 13: Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn...
Giải bài tập trang 113, 114 bài 1 Bảng phân bố tần số và tần suất Sách giáo khoa Đại số 10. Câu 1: Cho các số liệu thống kê ghi trong bảng sau...
Giải bài tập trang 118 bài 2 biểu đồ Sách giáo khoa (SGK) Đại số 10. Câu 1: Hãy mô tả bảng phân bố tần suất ghép lớp đã được lập ở bài tập số...
