Câu 1 trang 62 SGK Hình học 10

Hãy nhắc lại định nghĩa giá trị lượng giác của một  góc \(α\) với \(0^0≤  α ≤ 180^0\). Tại sao khi \(α\) là một góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?

Trả lời:

_ Định nghĩa: Với mỗi góc  \(α\) \(0^0≤  α ≤ 180^0\) ta xác định một điểm \(M\) trên nửa đường tròn đơn

vị sao cho góc \(xOM =  α\) và giả sử điểm \(M\) có tọa độ \(M (x_0;y_0)\).

Khi đó ta có định nghĩa:

Sin của góc \(α\) là \(y_0\), kí hiệu là \(\sin α = y_0\)

cosin của góc \(α\) là \(x_0\)_, kí hiệu là \(\cos α = x_0\)

tang của góc \(α\) là \(( x_0≠ 0)\), ký hiệu \(\tan α =  {{{y_0}} \over {{x_0}}}\)

cotang cuả góc \(α\) là \((y_0≠ 0)\), ký hiệu \(\cot α =  {{{x_0}} \over {{y_0}}}\)

Các số \(\sin α, \cos α, \tan α, \cot α\) được gọi là các giá trị lượng giác của góc \( α\).

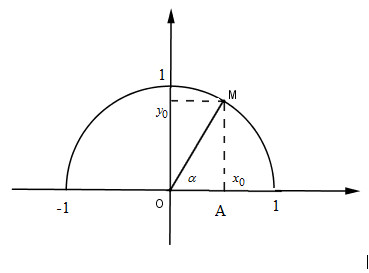
_ Khi \(α\) là các góc nhọn thì:

+ Theo định nghĩa ta có: \(\sin α = y_0\)

Trong tam giác \(OAM\) vuông tại \(A\), ta có: \(\sin \alpha  = {{{y_0}} \over 1} = {y_0}\)

+ Theo định nghĩa ta có: \(\cos α = x_0\)

Trong tam giác \(OAM\) vuông tại \(A\), ta có: \(\cos \alpha  = {{OA} \over {OM}} = {{{x_0}} \over 1} = {x_0}\)

+ Theo định nghĩa ta có: \(\tan \alpha  = {{{y_0}} \over {{x_0}}}({x_0} \ne 0)\)

Trong tam giác \(OAM\) vuông tại \(A\), ta có: \(\tan \alpha  = {{AM} \over {OA}} = {{{y_0}} \over {{x_0}}}\)

+ Theo định nghĩa ta có: \(\cot \alpha  = {{{x_0}} \over {{y_0}}}({y_0} \ne 0)\)

Trong tam giác \(OAM\) vuông tại \(A\), ta có:  \(\cot \alpha  = {{OA} \over {AM}} = {{{x_0}} \over {{y_0}}}\)

Câu 2 trang 62 SGK Hình học 10

Tại sao hai góc bù nhau lại có sin bằng nhau và cosin đối nhau?

Trả lời:

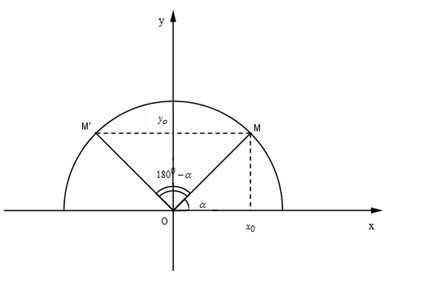
Hai góc bù nhau thì \(M\) và \(M’\) đối xứng với nhai qua trục \(Oy\) nên có sin bằng nhau và cosin đối

nhau. Hai điểm \(M\) và \(M’\) có cùng tung độ, còn hoành độ đối nhau. 

Câu 3 trang 62 SGK Hình học 10

Nhắc lại định nghĩa tích vô hướng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \). Tích vô hướng này với |\(\overrightarrow a \)  | và |\(\overrightarrow b \) | không đổi đạt giá trị lớn nhất và nhỏ nhẩt khi nào?

Trả lời:

Theo định nghĩa ta có: \(\overrightarrow a .\overrightarrow b  = |\overrightarrow a |.|\overrightarrow b |.cos(\overrightarrow a ,\overrightarrow b )\)

Vì \(|cos(\overrightarrow a ,\overrightarrow b )| \le 1\) nên:

+) \(\overrightarrow a .\overrightarrow b \) đạt giá trị lớn nhất \(|\overrightarrow a |.|\overrightarrow b |\) khi:

\(\cos (\overrightarrow a ,\overrightarrow b ) = 1 \Rightarrow (\overrightarrow a ,\overrightarrow b ) = {0^0}\)

 tức là  \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.

+) \(\overrightarrow a .\overrightarrow b \) đạt giá trị nhỏ nhất \(|\overrightarrow a |.|\overrightarrow b |\)  khi:

\(⇒   \cos (\overrightarrow a ,\overrightarrow b ) =  - 1 \Rightarrow (\overrightarrow a ,\overrightarrow b ) = {180^0}\) và \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng.

Câu 4 trang 62 SGK Hình học 10

Trong mặt phẳng \(Oxy\) cho vecto \(\overrightarrow a  = ( - 3;1)\) và vecto \(\overrightarrow b  = (2;2)\) . Hãy tính tích vô hướng \(\overrightarrow a .\overrightarrow b \) .

Trả lời:

Áp dụng công thức: 

Với \(\overrightarrow a  = ({a_1};{a_2});\overrightarrow b  = ({b_1};{b_2}) \Rightarrow \overrightarrow a .\overrightarrow b  = {a_1}{b_1} + {a_2}{b_2}\)

Ta có: \(\overrightarrow a .\overrightarrow b  = ( - 3).2 + 1.2 =  - 6 + 2 =  - 4\)

Giaibaitap.me