Bài 1 trang 49 sgk đại số 10

Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.

a) \(y = {x^2} - 3x + 2\);                                         

b) \(y =  - 2{x^2} + {\rm{ }}4x - 3\);

c) \(y= {x^2} - 2x\);                                               

d) \(y =  - {x^2} + 4\). 

Giải

a) \(y = {x^2} - 3x + 2\).

Hệ số: \(a = 1, b = - 3, c = 2\).

Hoành độ đỉnh \(x_1\)= \(-\frac{b}{2a}=\frac{3}{2}.\)

Tung độ đỉnh \(y_1\) = \(-\frac{\Delta }{4a}=\frac{4.2.1-(-3)^{2}}{4.1}=-\frac{1}{4}.\)

          Vậy đỉnh parabol là \(I(\frac{3}{2};-\frac{1}{4})\).

• Giao điểm của parabol với trục tung là \(A(0; 2)\).
• Hoành độ giao điểm của parabol với trục hoành là nghiệm của phương trình:

 \(x^2- 3x + 2 = 0\)

\( \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = 2 \hfill \cr} \right.\)

     Vậy các giao điểm của parabol với trục hoành là \(B(1; 0)\) và \(C(2; 0)\).

b) \(y =  - 2{x^2} + {\rm{ }}4x - 3\)

Hệ số: \(a=-2;b=4;c=-3\)

Hoành độ đỉnh \(x_1\)= \(-\frac{b}{2a}=1\)

Tung độ đỉnh \(y_1\) = \(-\frac{\Delta }{4a}=\frac{4.(-2).(-3)-4^{2}}{4.(-2)}=-1.\)

 Vậy đỉnh parabol là \(I(1;-1)\).

Giao điểm với trục tung \(A(0;- 3)\).

Phương trình  \(- 2x^2+ 4x - 3 = 0\) vô nghiệm. Không có giao điểm của parabol với trục hoành.

c) Đỉnh \(I(1;- 1)\). Các giao điểm với hai trục tọa độ: \(A(0; 0), B(2; 0)\).

d) Đỉnh \(I(0; 4)\). Các giao điểm với hai trục tọa độ: \(A(0; 4), B(- 2; 0), C(2; 0)\).

Bài 2 trang 49 SGK Đại số 10

 Lập bảng biến thiên và vẽ đồ thị của các hàm số.

a) \(y = 3x^2- 4x + 1\);             b) \(y = - 3x^2+ 2x – 1\);

c) \(y = 4x^2- 4x + 1\);             d) \(y = - x^2+ 4x – 4\);

e) \(y = 2x^2+ x + 1\);               f) \(y = - x^2+ x - 1\).

Giải

a) \(y = 3x^2- 4x + 1\)

Bảng biến thiên: 

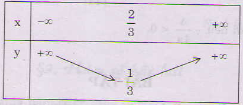
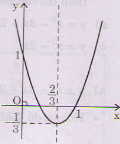
Đồ thị:

- Đỉnh: \(I\left( {{2 \over 3}; - {1 \over 3}} \right)\)

- Trục đối xứng: \(x = {2 \over 3}\)

- Giao điểm với trục tung \(A(0; 1)\)

- Giao điểm với trục hoành \(B\left( {{1 \over 3};0} \right)\), \(C(1; 0)\).

b) \(y = - 3x^2+ 2x – 1\)

Bảng biến thiên: 

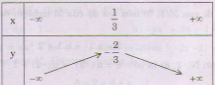
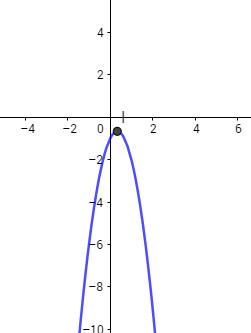
Vẽ đồ thị:

- Đỉnh \(I\left( {{1 \over 3}; - {2 \over 3}} \right)\), trục đối xứng: \(x = {1 \over 3}\)

- Giao điểm với trục tung \(A(0;- 1)\).

- Giao điểm với trục hoành: không có.

Ta xác định thêm điểm phụ: \(B(1;- 2)\), \(C(1;- 6)\).

c) \(y = 4x^2- 4x + 1\).

Lập bảng biến thiên và vẽ tương tự câu a, b.

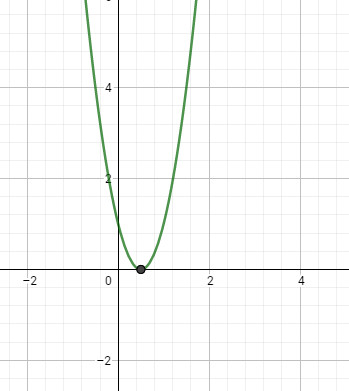
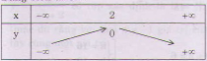
d) \(y = - x^2+ 4x – 4=- (x – 2)^2\)

Bảng biến thiên:

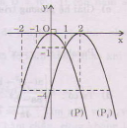
Cách vẽ đồ thị:

Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:

+ Vẽ đồ thị \((P)\) của hàm số \(y = - x^2\)^.

+ Tịnh tiến \((P)\) song song với \(Ox\) sang phải \(2\) đơn vị được \((P₁)\) là đồ thị cần vẽ. (hình dưới).

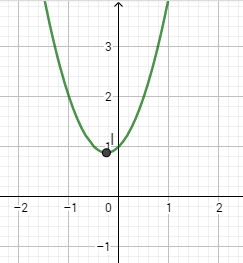
e)  \(y = 2x^2+ x + 1\);   

-          Đỉnh  \(I\left( {{{ - 1} \over 4};{{ - 7} \over 8}} \right)\)

-          Trục đối xứng :  \(x = {{ - 1} \over 4}\)

-          Giao \(Ox\): Đồ thị không giao với trục hoành

-          Giao \(Oy\): Giao với trục tung tại điểm \((0;1)\)

Bảng biến thiên:

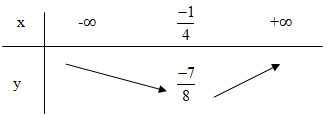
Vẽ đồ thị theo bảng sau:

f) \(y = - x^2+ x - 1\).

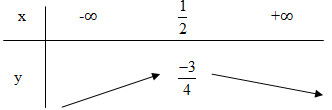
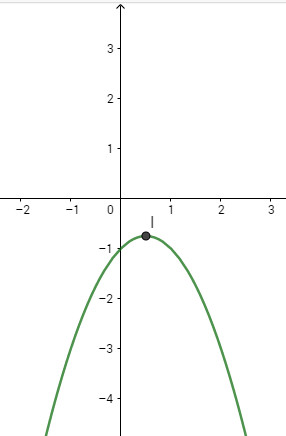
-          Đỉnh  \(I\left( {{1 \over 2};{{ - 3} \over 4}} \right)\)

-          Trục đối xứng :  \(x = {1 \over 2}\)

-          Giao Ox: Đồ thị không giao với trục hoành

-          Giao Oy: Giao với trục tung tại điểm \((0;-1)\)

Bảng biến thiên:

Vẽ đồ thị theo bảng sau:

Bài 3 trang 49 sgk đại số 10

Xác định parabol \(y = ax^2+ bx + 2\), biết rằng parabol đó:

a) Đi qua hai điểm \(M(1; 5)\) và \(N(- 2; 8)\);

b) Đi qua hai điểm \(A(3;- 4)\) và có trục đối xứng là \(x=-\frac{3}{2}.\)

c) Có đỉnh là \(I(2;- 2)\);

d) Đi qua điểm \(B(- 1; 6)\) và tung độ của đỉnh là \(-\frac{1}{4}.\)

Giải

a) Vì parabol đi qua \(M(1; 5)\) nên tọa độ của \(M\) là nghiệm đúng phương trình của parabol:  

        \(5 = a.1^2+ b.1 + 2\).

Tương tự, với \(N(- 2; 8)\) ta có:

         \(8 = a.(- 2)^2 + b.(- 2) + 2\) 

Giải hệ phương trình: \(\left\{\begin{matrix} a+b+2=5\\ 4a-2b+2=8 \end{matrix}\right.\) 

ta được \(a = 2, b = 1\).

Parabol có phương trình là: \(y = 2x^2 + x + 2\).

b) Vì parabol đi qua hai điểm \(A(3;- 4)\) nên tọa độ \(A\) là nghiệm đúng phương trình của parabol:

          \(a(3)^{2}+b.3+2=-4\)

Parabol có trục đối xứng là \(x=-\frac{3}{2}\) nên ta có:

           \(-\frac{b}{2a}=-\frac{3}{2}\)

Giải hệ phương trình: \(\left\{\begin{matrix} -\frac{b}{2a}=-\frac{3}{2}\\a(3)^{2}+b.3+2=-4 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=-\frac{1}{3}\\ b=-1 \end{matrix}\right.\)

Phương trình parabol cần tìm là: \(y = -\frac{1}{3} x^2- x + 2\).

c) Parabol có đỉnh \(I(2;- 2)\) do đó tọa độ \(I\) là nghiệm đúng phương trình của parabol:

      \(a.2^2+b.2+2=-2\)           

Parabol có đỉnh \(I(2;- 2)\) nên parabol có trục đối xứng là: \(x=2\) do đó:

       \( -\frac{b}{2a}=2\)          

Giải hệ phương trình: \(\left\{\begin{matrix} -\frac{b}{2a}=2\\a.2^2+b.2+2=-2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1\\ b=-4 \end{matrix}\right.\)

Phương trình parabol cần tìm là: \(y = x^2- 4x + 2\).

d)  Vì parabol đi qua điểm  \(B(- 1; 6)\) nên tọa độ \(B\) là nghiệm đúng phương trình của parabol:

         \(a(-1)^{2}+b(-1)+2=6\)

Parabol có tung độ của đỉnh là \(-\frac{1}{4}\) nên ta có:

         \(\frac{8a-b^{2}}{4a}=-\frac{1}{4} \)

Giải hệ phương trình ta được:

\(\left\{\begin{matrix} a(-1)^{2}+b(-1)+2=6\\ \frac{8a-b^{2}}{4a}=-\frac{1}{4} \end{matrix}\right.\Leftrightarrow \begin{bmatrix} \left\{\begin{matrix} a=16\\ b=12 \end{matrix}\right.\\ \left\{\begin{matrix} a=1\\ b=-3 \end{matrix}\right. \end{bmatrix}\)

Phương trình parabol cần tìm là: \(y = 16x^2+ 12x + 2\) hoặc \(y = x^2- 3x + 2\).

Bài 4 trang 50 sgk đại số 10

Xác định \(a, b, c\), biết parabol \(y = ax^2+ bx + c\) đi qua điểm \(A(8; 0)\) và có đỉnh \(I(6; - 12)\).

Giải

Parabol đi qua điểm \(A(8; 0)\) nên tọa độ điểm \(A\) là nghiệm đúng phương trình của parabol ta có:

      \(a.8^2+b.8+c=0\)

Parabol có đỉnh \(I(6; - 12)\) nên ta  có: 

       \( -\frac{b}{2a} =6 \)

       \(\frac{4ac-b^{2}}{4a} =-12 \)

Ta có hệ phương trình: \(\left\{\begin{matrix} a(8)^{2}+b(8)+c=0\\ -\frac{b}{2a} =6 \\\frac{4ac-b^{2}}{4a} =-12 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=3\\ b=-36 \\ c=96 \end{matrix}\right.\)

Phương trình parabol cần tìm là: \(y = 3x^2- 36x + 96\).

Giaibaitap.me