Bài 1 trang 41 SGK Đại số 10

 Vẽ đồ thị hàm số:

a) \(y = 2x - 3\);                                            b) \(y = \sqrt 2\);

c) \(y=-\frac{3x}{2}+7;\)                                        d) \(y = |x|\).

Giải

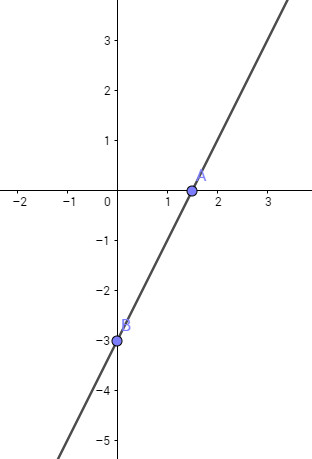
a) Đồ thị hàm số \(y = 2x - 3\) là đường thẳng đi qua hai điểm \(A(0; - 3)\) và \(B=\left ( -\frac{3}{2};0 \right )\)

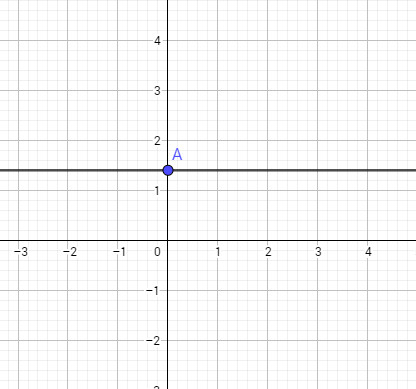
b) Đồ thị hàm số \(y = \sqrt 2\) là đường thẳng song song với trục hoành đi qua điểm \(A(0; \sqrt 2)\) 

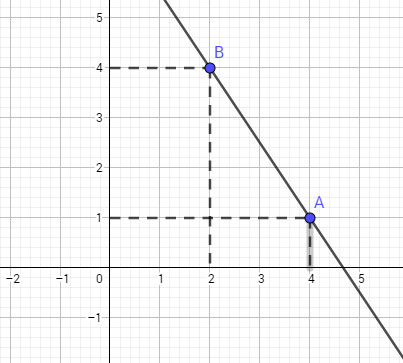
c) Đồ thị hàm số \(y=-\frac{3x}{2}+7\) là đường thẳng. Bởi vì giao điểm của đồ thị với trục tung \(P(0; 7)\) với trục hoành \(Q=(\frac{14}{3};0)\) có tọa độ  tương đối lớn nên ta có thể chọn các điểm thuộc đồ thị có tọa độ nhỏ hơn cho dễ vẽ. Chẳng hạn \(A(4; 1), B(2; 4)\). Đồ thị là đường thẳng AB 

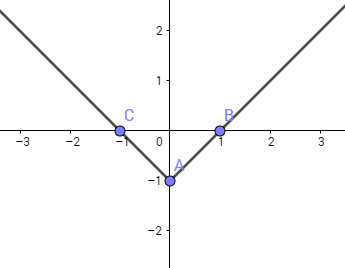
d)

\(y = |x| - 1 = \left\{ \matrix{
x - 1,x \ge 0 \hfill \cr
- x - 1,x < 0 \hfill \cr} \right.\)

Ta vẽ hai đường thẳng \(y=x-1\) với \(x\ge0\) và đường thẳng \(y=-x-1\) với \(x<0\)

Bài 2 trang 42 SGK Đại số 10

Xác định \(a, b\) để đồ thị của hàm số \(y = ax + b\) đi qua các điểm.

a) \(A(0; 3)\) và \(B=(\frac{3}{5};0)\);

b) \(A(1; 2)\) và \(B(2; 1)\);

c) \(A(15;- 3)\) và \(B(21;- 3)\).

Hướng dẫn.

a) Đồ thị hàm số \(y=ax+b\) đi qua \(A,B\) nên tọa độ của \(A,B\) thỏa mãn phương trình \(y=ax+b\)  ta được hệ phương trình: \(\left\{\begin{matrix} 3=a.0 + b\\ 0=a.\frac{3}{5}+b \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=-5\\ b=3 \end{matrix}\right.\)

Vậy phương trình của đường thẳng đi qua \(A(0; 3)\) và \(B=\left (\frac{3}{5};0 \right )\) là: \(y = - 5x + 3\).

 b) \(a= - 1, b= 3\).

Phương trình đường thẳng cần tìm là: \(y=-x+3\)

c) \(a= 0, b= - 3\).

Phương trình đường thẳng cần tìm là: \(y=-3\)

Bài 3 trang 42 sgk đại số 10

Viết phương trình \(y = ax + b\) của đường thẳng:

a) Đi qua điểm \(A(4; 3), B(2;- 1)\).

b) Đi qua điểm \(A(1;- 1)\) và song song với \(Ox\).

Giải

a) Phương trình đường thẳng \(y=ax+b\) đi qua \(A(4; 3)\) và \(B(2;- 1)\) nên tọa độ \(A,B\) thỏa mãn phương trình \(y=ax+b\). Do đó ta có:

 \(3 = a.4 + b\)  (1)

\(- 1 = a.2 + b\) (2)

Giải hệ (1) và (2) ta được: \(a=2,b=-5\)

Vậy phương trình đường thẳng \(AB\) cần tìm là: \(y = 2x - 5\).

b) Trục \(Ox\) có phương trình là \(y=0\). Đường thẳng \(y=ax+b\) song song với \(Ox\) nên \(a=0\), do đó đường thẳng cần tìm có dạng là \(y=b\)

Đường thẳng \(y=b\) đi qua \(A(1;-1)\) nên tọa độ \(A\) thỏa mãn phương trình đường thẳng, ta có: \(y=-1\)

Vậy phương trình đường thẳng cần tìm là: \(y=-1\)

Bài 4 trang 42 sgk đại số 10

Vẽ đồ thị hàm số.

a) 

\(y = \left\{ \matrix{
2x\text{ với }x \ge 0 \hfill \cr
- {1 \over 2}x\text{ với }x < 0 \hfill \cr} \right.\)

 b) 

\(y = \left\{ \matrix{
x + 1\text{ với }x \ge 1 \hfill \cr
- 2x + 4\text{ với }x < 1 \hfill \cr} \right.\)

Giải

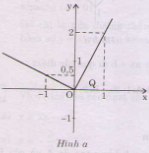
a) +) Vẽ đường thẳng \(y=2x\) với \(x\ge0\)

Đường thẳng \(y=2x\) đi qua hai điểm \(A(0;0)\) và \(B(1;2)\). Trên đường thẳng này ta giữ nguyên phần đường thẳng ứng với \(x\ge 0\) còn xóa bỏ phần còn lại ta được đồ thị của đường thẳng \(y=2x\) với \(x\ge0\).

     +) Vẽ đường thẳng \(y=- {1 \over 2}x\) với \(x<0\)

Đường thẳng \(y=- {1 \over 2}x\) đi qua hai điểm \(A(0;0)\) và \(B(-1;{1 \over 2})\). Trên đường thẳng này ta giữ nguyên phần ứng với \(x<0\) còn xóa bỏ phần còn lại ta được đồ thị của đường thẳng \(y=-{1 \over 2}x\)  với \(x<0\)  

Đồ thị của hàm số đã cho là hai đồ thị của hai hàm số \(y=2x\) với \(x\ge0\) và \(y=- {1 \over 2}x\) với \(x<0\)                 

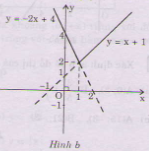
b) Tương tự phần a đồ thị của hàm số đã cho là hai đồ thị \(y=x + 1\) với  \(x \ge 1\) (phần nét liền) và \(y= - 2x + 4\) với  \(x < 1\) (phần nét liền)                  

Giaibaitap.me