Câu 1 trang 159 SGK Đại số 10

Hãy phát biểu các khẳng định sau đây dưới dạng điều kiện cần và đủ.

Tam giác $ABC$ vuông tại $A$ thì $BC^2= AB^2+AC^2$

Tam giác $ABC$ có các cách cạnh thỏa mãn hệ thức  $BC^2 = AB^2+AC^2$ thì vuông tại $A$.

Trả lời:

Điều kiện cần và đủ của tam giác $ABC$ vuông tại $A$ là các cạnh của nó thỏa mãn hệ thức :

 $a^2+ b^2 =c^2$

($a, b, c$ là độ dài các cạnh theo thứ tự đối diện các đỉnh $A, B, C$)

Câu 2 trang 159 SGK Đại số 10

Lập bảng biến thiên và vẽ đồ thị các hàm số.

a) $y = -3x+2$

b) $y = 2x^2$

c) $y = 2x^2– 3x +1$

Trả lời:

a) Bảng biến thiên

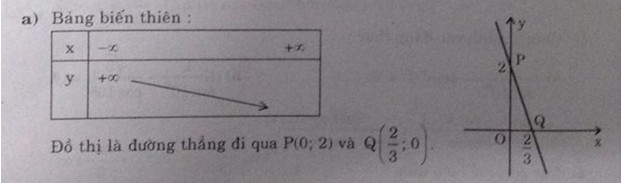
Đồ thị là đường thẳng đi qua $P(0; 2)$ và $Q({2 \over 3},0)$

c) Bảng biến thiên

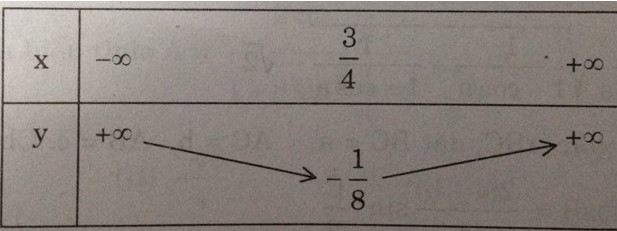
Đồ thị là parabol có đỉnh là $I({3 \over 4},{{ - 1} \over 8})$ , trục đối xứng $x = {3 \over 4}$ cắt trục tung tại $P(0; 1)$, cắt trục hoành tại các điểm có hoành độ là nghiệm của phương trình:

 $2{x^2} - 3x + 1 = 0 \Leftrightarrow {x_1} = {1 \over 2},{x_2} = 1$

tức là cắt trục hoành tại $A({1 \over 2},0)$ và $B(1;0)$

Câu 3 trang 159 SGK Đại số 10

Phát biểu quy tắc xét dấu một nhị thức bậc nhất. Áp dụng quy tắc đó để giải bất phương trình sau:

$f(x) = {{(3x - 2)(5 - x)} \over {(2 - 7x)}} \ge 0$

Trả lời:

Quy tắc xét dấu một nhị thức dựa trên định lí :

 “Nhị thức $f(x) = ax + b (a≠0)$ có dấu cùng với hệ số $a$ khi $x$  lấy giá trị trong khoảng $({{ - b} \over a}, + \infty )$ và trái dấu với hệ số $a$ khi $x$ lấy các giá trị thuộc khoảng $( - \infty ,{{ - b} \over a})$”.

Áp dụng: Ta lập bảng xét dấu của vế trái $f(x)$ của bất phương trình:

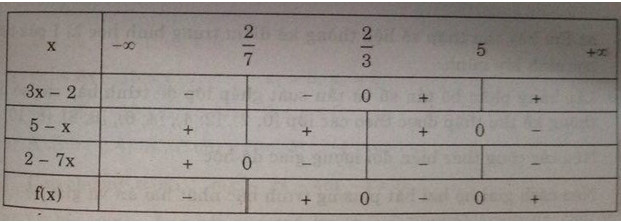
Tập nghiệm của bất phương trình: $S = ({2 \over 7},{2 \over 3}{\rm{] }} \cup {\rm{ [}}5, + \infty )$

Câu 4 trang 159 SGK Đại số 10

Phát biểu định lí về dấu của một tam thức bậc hai $f(x) = ax^2+ bx + c$.

Áp dụng quy tắc đó, hãy xác định giá  trị của $m$ để tam thức sau luôn luôn âm: 

$f(x) =  - 2{x^2} + 3x + 1 - m$                                                     

Trả lời:

Định lí: Tam thức bậc hai $f(x) = ax^2+ bx + c (a ≠0)$

có biệt thức $Δ = b^2– 4ac$

- Nếu $Δ < 0$ thì $f(x)$ cùng dấu với hệ số $a$với mọi $x∈\mathbb R$

- Nếu $Δ = 0$ thì $f(x)$ luôn cùng dấu với hệ số $a$ với mọi  $x \ne {{ - b} \over {2a}}$

- Nếu $Δ >0$ thì $f(x)$ có hai nghiệm $x_1;x_2$ ($x_1<x_2$)

    $f(x)$ cùng dấu với hệ số $a$ khi  $x<x_1$ hoặc  $x>x_2$

     $f(x)$ trái dấu với hệ số $a$ khi  $x_1<x<x_2$

Áp dụng: $f(x) =  - 2{x^2} + 3x + 1 - m$ có hệ số $a = -2<0$

Biệt thức: $Δ = 3^2- 4 .(- 2) (1-m) = 17 - 8m$

Tam thức $f(x)$ luôn âm (tức $f(x) < 0 , ∀x  ∈\mathbb R$ khi:

$\eqalign{ & \Delta < {\rm{ }}0 \Leftrightarrow 17 - 8m < 0 \cr & \Leftrightarrow m > {{17} \over 8} \cr}$

 Giaibaitap.me