Câu 5 trang 160 SGK Đại số 10

Giải hệ phương trình sau bằng cách đưa về hệ phương trình dạng tam giác:

\(\left\{ \matrix{
x + 3y + 2z = 1 \hfill \cr
3x + 5y - z = 9 \hfill \cr
5x - 2y - 3z = - 3 \hfill \cr} \right.\)  (I)

Trả lời:

Nhân phương trình thứ nhất với \(-3\) rồi cộng vào phương trình thứ hai.

Lại nhân phương trình thứ nhất rồi cộng vào phương trình thứ ba thì được hệ:

\((I) ⇔ (II)\) 

\(\left\{ \matrix{
x + 3y + 2z = 1 \hfill \cr
- 4y - 7z = 6 \hfill \cr
- 17y - 13z = - 8 \hfill \cr} \right.\)

Nhân phương trình thứ hai của hệ \((II)\) với \(17\), nhân phương trình thứ ba của hệ \((II)\) với \((-4)\) rồi cộng hai phương trình đó lại ta được:

\((II) ⇔ (III)\)

\(\left\{ \matrix{
x + 3y + 2z = 1 \hfill \cr
- 4y - 7z = 6 \hfill \cr
- 67z = 134 \hfill \cr} \right.\)

Hệ phương trình \((III)\) có dạng tam giác. Tìm giá trị các ẩn ngược từ dưới lên dễ dàng tìm được nghiệm của hệ phương trình đã cho:

\((x; y; z) = (-1; 2; -2)\)

Câu 6 trang 160 SGK Đại số 10

a) Xét dấu biểu thức

\(f(x) = 2x(x+2) – (x+2)(x+1)\)

b) Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc các đồ thị của các hàm số sau

\(y = 2x(x+2) (C_1)\)

\(y = (x+2)(x+1) (C_2)\)

Tính tọa độ các giao điểm \(A\) và \(B\) của \((C_1)\) và \((C_2)\)

c) Tính các hệ số \(a, b, c\) để hàm số \(y = ax^2+ bx + c\) có giá trị lớn nhất bằng \(8\) và đồ thị của nó đi qua \(A\) và \(B\).

Trả lời:

a) \(f(x) = (x+2)(x-1)\)

\(f(x) > 0\) với \(x < -2\) hoặc \(x > 1\)

\(f(x) ≤  0\) với \(-2 ≤ x ≤ 1\)

b) \(y = 2x (x + 2) = 2(x+1)^2– 2\)

Bảng biến thiên:

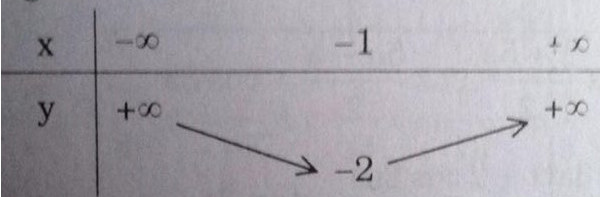
Hàm số : \(y{\rm{ }} = \left( {x + 2} \right)\left( {x + 1} \right) = {(x + {3 \over 2})^2} - {1 \over 4}\)

Bảng biến thiên

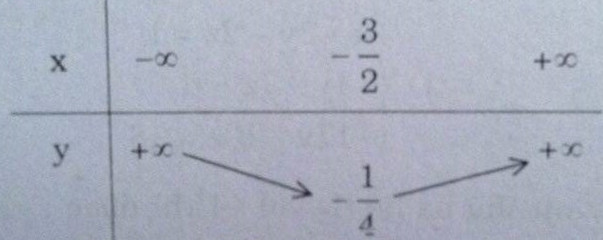
Đồ thị (C₁) và (C₂)

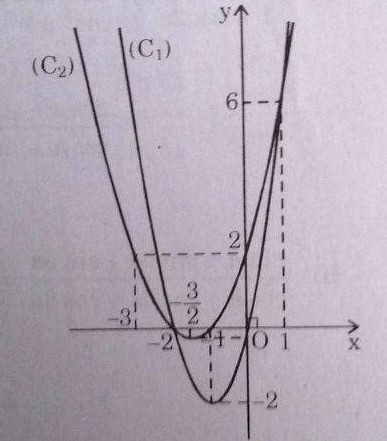
Hoành độ các giao điểm \(A\) và \(B\) của (C₁) và (C₂) là nghiệm của phương trình \(f(x) = 0  ⇔ x_1= -2, x_2= 1\)

\(⇔ A(-2; 0) , B(1; 6)\)

c) Giải hệ phương trình

\(\left\{ \matrix{
{{ac - {b^2}} \over {4a}} \hfill \cr
a{( - 2)^2} + b( - 2) + c = 0 \hfill \cr
a{(1)^2} + b(1) + c = 6 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = - 2,b = 0,c = 8 \hfill \cr
a = - {2 \over 9},b = {{16} \over 9},c = {{40} \over 9} \hfill \cr} \right.\)

Câu 7 trang 161 Đại số 10

Chứng minh các hệ thức sau:

a) \({{1 - 2{{\sin }^2}a} \over {1 + \sin 2a}} = {{1 - \tan a} \over {1 + \tan a}}\)

b) \({{\sin a + \sin 3a + \sin 5a} \over {\cos a + \cos 3a + \cos 5a}} = \tan 3a\)

c) \({{{{\sin }^4}a - {{\cos }^4}a + {{\cos }^2}a} \over {2(1 - \cos a)}} = {\cos ^2}{a \over 2}\)

d) \({{\tan 2x\tan x} \over {\tan 2x - \tan x}} = \sin 2x\)

Trả lời:

a)

\(\eqalign{
& {{1 - 2{{\sin }^2}a} \over {1 + \sin 2a}} = {{{{\cos }^2}a - {{\sin }^2}a} \over {{{\cos }^2}a + {{\sin }^2}a + 2\sin a\cos a}} \cr
& = {{\cos a - \sin a} \over {\cos a + \sin a}} = {{1 - {{\sin a} \over {\cos a}}} \over {1 + {{\sin a} \over {\cos a}}}} \cr
& = {{1 - \tan a} \over {1 + \tan a}} \cr} \)

b)

\(\eqalign{
& {{\sin a + \sin 3a + \sin 5a} \over {\cos a + \cos 3a + \cos 5a}} \cr
& = {{2\sin {{a + 5a} \over 2}\cos {{5a - a} \over 2} + \sin 3a} \over {2\cos {{a + 5a} \over 2}\cos {{5a - a} \over 2} + \cos 3a}} = {{\sin 3a(1 + 2\cos 2a)} \over {\cos 3a(1 + 2\cos 2a)}} \cr
& = \tan 3a \cr} \)

c)

\(\eqalign{
& {{{{\sin }^4}a - {{\cos }^4}a + {{\cos }^2}a} \over {2(1 - \cos a)}} = {{({{\sin }^2}a + {{\cos }^2}a)({{\sin }^2}a - {{\cos }^2}a) + {{\cos }^2}a} \over {2(1 - \cos a)}} \cr
& = {{{{\sin }^2}a - {{\cos }^2}a + {{\cos }^2}a} \over {4{{\sin }^2}{a \over 2}}} = {{4{{\sin }^2}{a \over 2}{{\cos }^2}{a \over 2}} \over {4{{\sin }^2}{a \over 2}}} \cr
& = {\cos ^2}{a \over 2} \cr} \)

d) 

\(\eqalign{
& {{\tan 2x\tan x} \over {\tan 2x - \tan x}} \cr
& = {{{{2\tan x} \over {1 - {{\tan }^2}x}}.\tan x} \over {{{2\tan x} \over {1 - {{\tan }^2}x}} - \tan x}} = {{2\tan x} \over {{{\tan }^2}x + 1}} \cr
& = \sin 2x \cr} \)

Câu 8 trang 161 SGK Đại số 10

Rút gọn các biểu thức sau:

a) \({{1 + \sin 4a - \cos 4a} \over {1 + \cos 4a + \sin 4a}}\)

b) \({{1 + \cos a} \over {1 - \cos a}}{\tan ^2}{a \over 2} - {\cos ^2}a\)

c) \({{\cos 2x - \sin 4x - \cos 6x} \over {\cos 2x + \sin 4x - \cos 6x}}\)

Trả lời:

a)

\(\eqalign{
& {{1 + \sin 4a - \cos 4a} \over {1 + \cos 4a + \sin 4a}} = {{2{{\sin }^2}2a + 2\sin 2a\cos 2a} \over {2{{\cos }^2}2a + 2\sin 2a\cos 2a}} \cr
& = {{2\sin 2a(\sin 2a + \cos 2a)} \over {2\cos 2a(\sin 2a + \cos 2a)}} = \tan 2a \cr} \)

b) 

\(\eqalign{
& {{1 + \cos a} \over {1 - \cos a}}{\tan ^2}{a \over 2} - {\cos ^2}a = {{2{{\cos }^2}{a \over 2}} \over {2{{\sin }^2}{a \over 2}}}.{{2{{\sin }^2}{a \over 2}} \over {2{{\cos }^2}{a \over 2}}} - {\cos ^2}{a \over 2} \cr
& = 1 - {\cos ^2}{a \over 2} = {\sin ^2}{a \over 2} \cr} \)

c) 

\(\eqalign{
& {{\cos 2x - \sin 4x - \cos 6x} \over {\cos 2x + \sin 4x - \cos 6x}} = {{(cos2x - \cos 6x) - sin4x} \over {(cos2x - \cos 6x) + sin4x}} \cr
& = {{-2\sin {{2x + 6x} \over 2}\sin {{6x - 2x} \over 2} - \sin 4x} \over {-2\sin {{2x + 6x} \over 2}\sin {{2x - 6x} \over 2} + \sin 4x}} \cr
& = {{2\sin 2x - 1} \over {2\sin 2x + 1}} \cr} \)

Giaibaitap.me