Câu 9 trang 107 SGK Đại số 10

Phát biểu định lí về dấu của tam thức bậc hai.

Trả lời:

+) Nếu biệt số \(Δ\) của tam thức bậc hai \(f(x) = ax^2+bx+c (a ≠0)\) là số âm thì \(a.f(x)>0, ∀x\in \mathbb R\)

+) Nếu \(Δ=0\) thì \(a.f(x) >0,∀x\in \mathbb R \backslash\left\{{{ - b} \over {2a}}\right\}\)

+) Nếu biệt số \(Δ>0\) thì

 i) \(a.f(x)>0\) khi \(x ∉[x_1;x_2]\)

 ii) \(a.f(x)>0\) khi \(x \in (x_1;x_2)\)

(\(x_1;x_2\) là hai nghiệm của \(f(x)\) với \(x_1<x_2\))

Câu 10 trang 107 SGK Đại số 10

Cho \(a>0, b>0\). Chứng minh rằng: \({a \over {\sqrt b }} + {b \over {\sqrt a }} \ge \sqrt a  + \sqrt b \)

Trả lời:

Đặt \(x=\sqrt a, y = \sqrt b\) ( ta có \(x>0\) và \(y>0\))

 \({a \over {\sqrt b }} = {{{x^2}} \over y};{b \over {\sqrt a }} = {{{y^2}} \over x}\)

Suy ra: \({a \over {\sqrt b }} + {b \over {\sqrt a }} = {{{x^2}} \over y} + {{{y^2}} \over x} = {{{x^3} + {y^3}} \over {xy}} = {{(x + y)({x^2} + {y^2} - xy)} \over {xy}}\) (1)

Mà \(x^2+y^2≥ 2xy\) (Bất đẳng thức Cô-si)

Nên \(x^2+y^2- xy ≥ xy ⇔\) \({{{x^2} + {y^2} - xy} \over {xy}} \ge 1\)

Do đó (1) \({{{x^3} + {y^3}} \over {xy}}≥ x+y ⇔ {{{x^2}} \over y} + {{{y^2}} \over x} \ge x + y\)

\(⇔ {a \over {\sqrt b }} + {b \over {\sqrt a }} \ge \sqrt a  + \sqrt b \)

Câu 11 trang 107 SGK Đại số 10

a) Bằng cách sử dụng hằng đẳng thức \(a^2-b^2= (a-b)(a+b)\),

hãy xét dấu \(f(x)= x^4– x^2+6x – 9\) và \(g(x) = x^2– 2x - {4 \over {{x^2} - 2x}}\)

b) Hãy tìm nghiệm nguyên của bất phương trình sau: \(x(x^3– x + 6) > 9\)

Trả lời:

a) \(f(x) = {x^4} - {x^2} + 6x - 9 = {\left( {{x^2}} \right)^2} - {\left( {x - 3} \right)^2} = \left( {{x^2} + x - 3} \right)\left( {{x^2} - x + 3} \right)\)

\({{x^2} - x + 3} > 0, ∀x ∈\mathbb R\) ( vì \(a = 1> 0, Δ = 1- 4.3<0\))

Suy ra \(f(x)>0\) với \(x < {{ - 1 - \sqrt {13} } \over 2}\) hoặc \(x > {{ - 1 + \sqrt {13} } \over 2}\)

\(g(x) = x^2– 2x -  {4 \over {{x^2} - 2x}}\) 

= \({{{{({x^2} - 2x)}^2} - {2^2}} \over {{x^2} - 2x}} = {{({x^2} - 2x + 2)({x^2} - 2x - 2)} \over {{x^2} - 2x}}\)

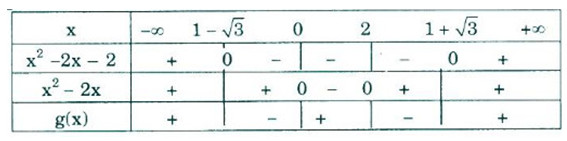
Bởi vì \(x^2– 2x + 2 > 0 ,∀x ∈\mathbb R\) nên dấu của \(g(x)\) là dấu của \({{{x^2} - 2x - 2} \over {{x^2} - 2x}}\)

Lập bảng xét dấu:

b) 

\(\eqalign{
& x({x^3} - x + 6) > 9 \Leftrightarrow {x^4} - {x^2} + 6x - 9 > 0 \cr
& \Leftrightarrow {x^4} - {(x - 3)^2} > 0 \Leftrightarrow ({x^2} - x + 3)({x^2} + x - 3) > 0 (1) \cr} \)

Vì \({{x^2} - x + 3} > 0, ∀x ∈\mathbb R\) ( vì \(a = 1> 0, Δ = 1- 4.3<0\))

Do đó (1) \(\Leftrightarrow ({x^2} + x - 3) > 0 \)

                \( \Leftrightarrow \left[ \matrix{
x < {{ - 1 - \sqrt {13} } \over 2} \hfill \cr
x > {{ - 1 + \sqrt {13} } \over 2} \hfill \cr} \right.\)

Vậy nghiệm nguyên của bất phương trình là \(\left\{x\in \mathbb Z|x\le-3\text{ hoặc } x\ge2\right\}\)

Câu 12 trang 107 SGK Đại số 10

Cho \(a, b, c\) là độ dài ba cạnh của một tam giác. Sử dụng định lí về dấu của tam thức bậc hai , chứng minh rằng: \({b^2}{x^{2}}-{\rm{ }}({b^2} + {c^2}-{\rm{ }}{a^2})x{\rm{ }} + {c^2} > 0,{\rm{ }}\forall x\)

Trả lời:

Biệt thức của tam thức vế  trái:

\({\Delta {\rm{ }} = {\rm{ }}{{\left( {{b^2} + {c^2}-{\rm{ }}{a^2}} \right)}^2}-{\rm{ }}4{b^2}{c^2}}\)

\({ = {\rm{ }}\left( {{b^2} + {c^2}-{\rm{ }}{a^{2}} + {\rm{ }}2bc} \right){\rm{ }}\left( {{b^2} + {c^2}-{\rm{ }}{a^2} - 2bc} \right)}\)

\({ = {\rm{ }}\left[ {{{\left( {b + c} \right)}^2}-{\rm{ }}{a^2}} \right]\left[ {{{\left( {b - c} \right)}^2}-{\rm{ }}{a^2}} \right]}\)

\({ = {\rm{ }}\left( {b + a + c} \right)\left( {b + c{\rm{ }}-{\rm{ }}a} \right)\left( {b{\rm{ }}-{\rm{ }}c + a} \right)\left( {b{\rm{ }}-{\rm{ }}c{\rm{ }}-{\rm{ }}a} \right){\rm{ }} < 0}\)

(vì trong một tam giác tổng của hai cạnh lớn hơn cạnh thứ ba \(b+a+c>0; b+c – a>0; b – c+a>0; b – c – a<0\))

Do đó tam giác cùng dấu với \(b^2>0, ∀x\).

Nghĩa là: \({b^2}{x^{2}}-{\rm{ }}({b^2} + {c^2}-{\rm{ }}{a^2})x{\rm{ }} + {c^2} > 0,{\rm{ }}\forall x\)

Giaibaitap.me