Bài 7 trang 69 sgk Toán 9 - tập 1

Bài 7. Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là \({x^2} = ab\) ) như trong hai hình sau:

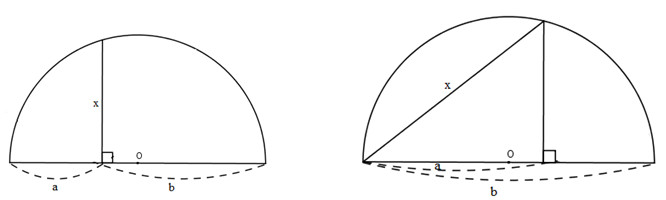
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.

Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

Hướng dẫn giải:

Cách 1: Đặt tên các đoạn thẳng như hình bên. 

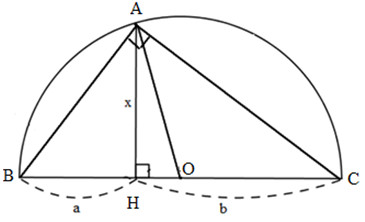
Xét tam giác ABC ta có:

\(OA = OB = OC = {{BC} \over 2}\left( { = R} \right)\)

Suy ra ∆ABC vuông tại A.

Áp dụng hệ thức \({h^2} = b'c' \Rightarrow {x^2} = ab\)

Cách 2: Vẽ và đặt tên như hình bên dưới

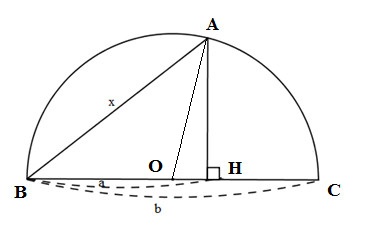
Xét tam giác ABC ta có:

\(OA = OB = OC = {{BC} \over 2}\left( { = R} \right)\)

Suy ra ∆ABC vuông tại A.

Áp dụng hệ thức \(A{B^2} = BC.BH \Rightarrow {x^2} = ab\).

Bài 8 trang 70 sgk Toán 9 - tập 1

Bài 8. Tìm x và y trong mỗi hình sau:

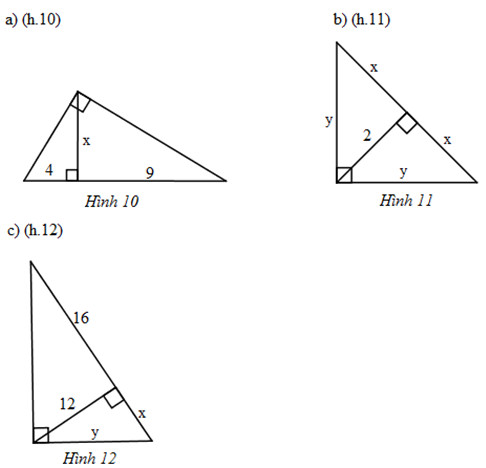
Hướng dẫn giải:

a) Dùng hệ thức lượng bình phương đường cao bằng tích hai hình chiếu hai cạnh góc vuông lên cạnh huyền \(h^{2}=b'c'\)

\(\eqalign{
& \Rightarrow {x^2} = 4.9 = 36 \cr
& \Rightarrow x = 6 \cr} \)

b) Xét tam giác ABC có cạnh huyền là 2x, ta nhận thấy rằng, tam giác này là tam giác vuông cân. Mặc khác, đường cao của tam giác này có độ lớn bằng 2 nên:

\(\frac{1}{y^2}+\frac{1}{y^2}=\frac{1}{2^2}\Rightarrow y=2\sqrt{2}\)

Cạnh huyền của tam giác lớn có độ lớn là 2x, áp dụng định lí Pytago vào tam giác vuông lớn, ta có:

\(2x=\sqrt{y^2+y^2}=\sqrt{8+8}=4\Rightarrow x=2\)

c) Xét tam giác vuông lớn, ta có:

\(12^2=16x\Rightarrow x=9\)

Xét tam giác vuông có cạnh huyền là y, ta có:

\(y^2=\sqrt{12^2+9^2}=15\)

Bài 9 trang 70 sgk Toán 9 - tập 1

Bài 9. Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và Tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông goác với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng

a) Tam giác DIL là một tam giác cân;

b) Tổng \(\frac{1}{DI^{2}}+\frac{1}{DK^{2}}\) không đổi khi I thay đổi trên cạnh AB.

Hướng dẫn giải:

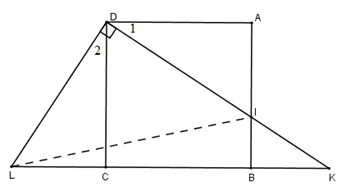
a) \(\Delta ADI\) và \(\Delta CDL\) có:

\(\widehat{A}=\widehat{C}= 90^{\circ}\)

\(AD=CD\) (hai cạnh hình vuông)

\(\widehat{D_{1}}=\widehat{D_{2}}\) cùng phụ với \(\widehat{CDI}\)

Do đó \(\Delta ADI=\Delta CDL\) (g.c.g)

Suy ra \(DI=DL\). Vậy \(\Delta DIL\) cân

b) Áp dụng hệ thức \(\frac{1}{h^{2}}=\frac{1}{b^{2}}+\frac{1}{c^{2}}\) ta có \(\frac{1}{DC^{2}}=\frac{1}{DL^{2}}+\frac{1}{DK^{2}}\)

Do đó \(\frac{1}{DC^{2}}=\frac{1}{DI^{2}}+\frac{1}{DK^{2}}\)

Do DC không đổi nên \(\frac{1}{DI^{2}}+\frac{1}{DK^{2}}\) là không đổi.

Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức \(\frac{1}{h^{2}}=\frac{1}{b^{2}}+\frac{1}{c^{2}}\)

Nếu đề bài không cho vẽ \(DL\perp DK\) thì ta vẫn phải vẽ đường phụ \(DL\perp DK\) để có thể vận dụng hệ thức trên.

Giaibaitap.me