Bài 10 trang 76 sgk Toán 9 - tập 1

Bài 10. Vẽ một tam giác vuông có một góc nhọn \(34^{\circ}\) rồi viết các tỉ số lượng giác của góc \(34^{\circ}\).

Hướng dẫn giải:

Vẽ tam giác ABC vuông tại A, \(\widehat{C}=34^{\circ}\)

Để vẽ được tam giác đề yêu cầu, chúng ta thực hiện các bước như sau:

B1. Vẽ đoạn thẳng AB với độ dài bất kì.

B2. Từ A dựng tia Ax vuông góc với đoạn thẳng AB

B3. Từ B dùng thước đo góc vẽ tia By sao cho góc ABy bằng 34 độ.

B4. Ax và By cắt nhau tại C.

B5. Vẽ tam giác ABC

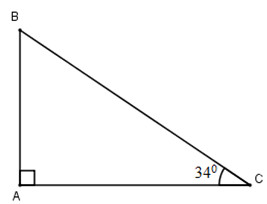
Tỉ số lượng giác của góc 34 độ là:

\(sin34^o=\frac{AC}{BC}\)

\(cos34^o=\frac{AB}{BC}\)

\(tg34^o=\frac{AC}{AB}\)

\(cot34^o=\frac{AB}{AC}\)

Bài 11 trang 76 sgk Toán 9 - tập 1

Bài 11. Cho tam giác ABC vuông tại C, trong đó \(AC=0,9m\), \(BC=1,2m\). Tính các tỷ số lượng giác của góc B, từ đó suy ra các tỷ số lượng giác của góc A.

Hướng dẫn giải:

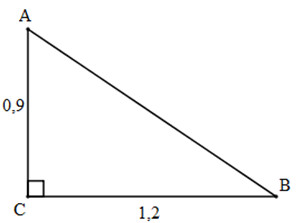
Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:

\(AB=\sqrt{AC^2+BC^2}=\sqrt{0,9^2+1,2^2}=1,5\)

Từ đó, ta có:

\(sinA=cosB=\frac{BC}{AB}=\frac{4}{5}\)

\(sinB=cosA=\frac{AC}{AB}=\frac{3}{5}\)

\(tgA=cotB=\frac{BC}{AC}=\frac{4}{3}\)

\(tgB=cotA=\frac{AC}{BC}=\frac{3}{4}\)

Nhận xét: Với hai góc phụ nhau, ta có sin góc này bằng cosin góc kia, tg góc này bằng cotan góc kia!

Bài 12 trang 76 sgk Toán 9 - tập 1

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn \(45^{\circ}\):

\(sin 60^{\circ},\,\,\,cos75^{\circ}, \,\,\,sin52^{\circ}30', \,\,\,cotg82^{\circ},\,\,\, tg80^{\circ}.\)

Giải:

Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:

\(sin60^o=cos(90^o-60^o)=cos30^o\)

\(cos75^o=sin(90^o-75^o)=sin15^o\)

\(sin52^o30'=sin52,5^o=cos(90^o-52,5^o)=cos37,5^o\)

\(cot82^o=tan(90^o-82^o)=tan8^o\)

\(tan80^o=cot(90^o-80^o)=cot10^o\)

Bài 13 trang 77 sgk Toán 9 - tập 1

Bài 13. Dựng góc nhọn \(\alpha\) , biết:

a) \(sin\alpha =\frac{2}{3}\)

b) \(cos\alpha =0,6\)

c) \(tg\alpha =\frac{3}{4}\)

d) \(cotg\alpha =\frac{3}{2}\)

Hướng dẫn giải:

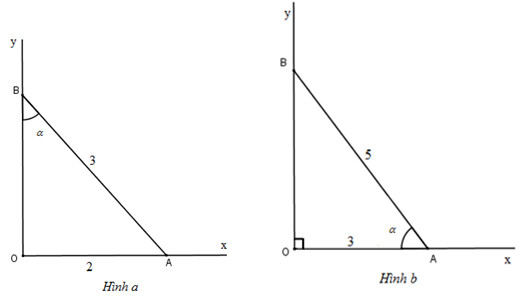
a) (H.a)

- Dựng góc vuông xOy.

-Trên tia Ox đặt OA=2

- Dựng đường tròn (A;3) cắt tia Oy tại B

Khi đó \(\widehat{OBA}=\alpha\)

Thật vậy \(sin\alpha =\frac{OA}{OB}=\frac{2}{3}\).

b) (H.b)

Tương tự câu a, ta sẽ tính độ lớn cạnh góc vuông còn lại bằng Pytago:

\(=\sqrt{5^2-3^2}=4\)

Vậy ta sẽ vẽ một góc vuông, và vẽ hai độ lớn là \(3\) và \(4\)

Hình trên cho ta thấy:

\(cos\alpha =cosABC=\frac{3}{5}\)

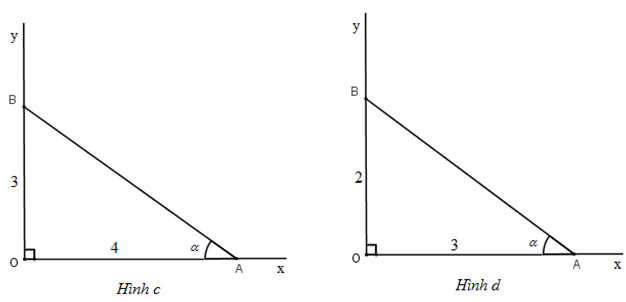
c) Vẽ tam giác vuông có hai cạnh có độ lớn là \(3\) và \(4\)

Hình trên cho ta thấy:

\(tg\alpha =tgACB=\frac{3}{4}\)

d) Vẽ tam giác vuông có hai cạnh có độ lớn là \(3\) và \(2\)

Hình trên cho ta thấy:

\(cot\alpha =cotABC=\frac{3}{2}\)

Giaibaitap.me