Bài 14 trang 77 sgk Toán 9 - tập 1

Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn \(\alpha\) tùy ý, ta có:

a)\(tg\alpha =\frac{sin\alpha }{cos\alpha};\)

\(cotg\alpha =\frac{cos\alpha }{sin\alpha };tg\alpha\cdot cotg\alpha =1\).

b) \(sin\alpha ^{2}+cos\alpha ^{2}=1\)

Gợi ý: Sử dụng định lý Py-ta-go.

Hướng dẫn giải:

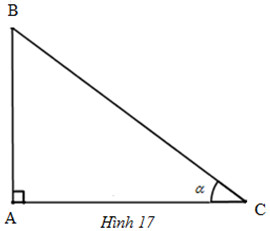
a) \(tg\alpha =\frac{AB}{AC}=\frac{AB\cdot BC}{AC\cdot BC}\)

\(\Rightarrow tg\alpha =\frac{AB}{BC}\div \frac{AC}{BC}=\frac{sin\alpha }{cos\alpha }\)

\(tg\alpha \cdot cotg\alpha =\frac{AB}{AC}\cdot \frac{AC}{AB}=1\)

\(cotg\alpha =\frac{1}{tg\alpha }=\frac{1}{\frac{sin\alpha }{cos\alpha }}=\frac{cos\alpha }{sin\alpha }\)

b) \(sin ^{2}\alpha +cos^{2}\alpha =\frac{AB^{2}}{BC^{2}}+\frac{AC^{2}}{BC^{2}}=\frac{BC^{2}}{BC^{2}}=1\)

Nhận xét: Ba hệ thức:

\(tg\alpha =\frac{sin\alpha }{cos\alpha }\);

\(cotg\alpha =\frac{cos\alpha }{sin\alpha };\)

\(sin^{2}\alpha +cos^{2}\alpha =1\) là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.

Bài 15 trang 77 sgk Toán 9 - tập 1

Cho tam giác ABC vuông tại A. Biết cos B=0,8, hãy tính các tỷ số lượng giác của góc C.

Gợi ý: Sử dụng bài tập 14.

Hướng dẫn giải:

Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:

\(sinC>0;\,\,\,cosC>0;\,\,\,tanC>0;\,\,\,cotC>0\)

Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.

Ta có:

\(Sin^{2}C+cos^{2}C=1\)

\(\Rightarrow cos^{2}C=1-sin^{2}C=1-(0,8)^{2}=0,36\)

\(\Rightarrow cosC=0,6;\)

\(tgC=\frac{sinC}{cosC}=\frac{0,8}{0,6}=\frac{4}{3};\)

\(cotgC=\frac{cosC}{sinC}=\frac{0,6}{0,8}=\frac{3}{4}\)

Nhận xét: Nếu biết  \(sin\alpha\) (hay \(cos\alpha\)) thì ta có thể tính được ba tỷ số lượng giác còn lại.

Bài 16 trang 77 sgk Toán 9 - tập 1

Bai 16: Cho tam giác vuông có một góc bằng \(60^{\circ}\) và cạnh huyền có độ dài bằng 8. Hãy tìm độ dài của cạnh đối diện góc \(60^{\circ}\).

Hướng dẫn giải:

Xem hình dưới:

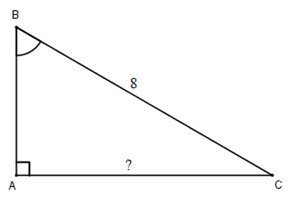
Bài toán yêu cầu tính cạnh AC

Nhìn vào hình vẽ, ta thấy hệ thức liên quan đến cạnh AC cần tìm, cạnh huyền BC cho trước, và góc ABC bằng 60 độ cho trước, ta có:

\(sinB=\frac{AC}{BC}\Rightarrow AC=BC\cdot sinB=8\cdot sin60^{\circ}=4\sqrt{3}\).

Bài 17 trang 77 sgk Toán 9 - tập 1

Bài 17: Tìm giá trị của x trong hình 23:

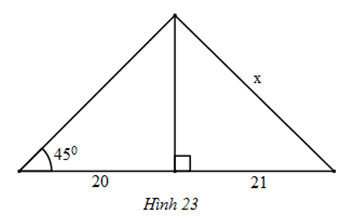
Giải:

Vẽ lại hình và đặt tên các góc như hình sau:

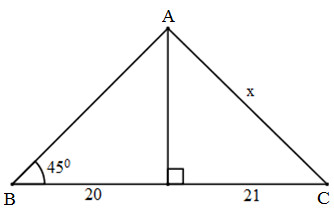
Vậy độ dài AC chính là x cần tìm.

Xét tam giác BHA vuông tại H có:

\(\left\{\begin{matrix} \widehat{ABC}=45^o\\ BH\perp HA \end{matrix}\right.\)

Vậy tam giác ABH vuông cân tại H.

\(\Rightarrow BH=AH=20\)

Áp dụng định lí Pytago vào tam giác AHC vuông tại H ta có:

\(AC=\sqrt{AH^2+HC^2}=\sqrt{20^2+21^2}=29\)

Vậy \(x=29\)

Giaibaitap.me