Bài 7 trang 38 sgk Toán 9 tập 2

Bài 7. Trên mặt phẳng tọa độ (h.10), có một điểm \(M\) thuộc đồ thị của hàm số \(y = a{x^2}\).

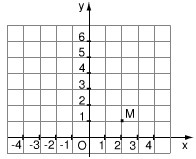
a) Tìm hệ số \(a\)

b) Điểm \(A(4; 4)\) có thuộc đồ thị không ?

c) Hãy tìm thêm hai điểm nữa (không kể điểm O) để vẽ đồ thị.

Bài giải:

a) Theo hình vẽ ta có tọa độ của điểm \(M\) là \(x = 2, y = 1\). \(M(2; 1)\) thuộc đồ thị hàm số \(y = a{x^2}\) nên ta có: \(1 = a{.2^2} \Leftrightarrow a = {1 \over 4}\)

b) Theo câu a, ta có hàm số là \(y = {1 \over 4}{x^2}\)

Thay tọa độ của điểm \(A\) vào hàm số ta được \(4 = {1 \over 4}{4^2}\) hay \(4 = 4\), thỏa mãn.

Vật điểm \(A(4; 4)\) thuộc đồ thị hàm số \(y = {1 \over 4}{x^2}\).

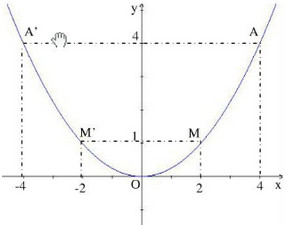
c) Nhờ tính đối xứng của đồ thị, chẳng hạn ta lấy thêm hai điểm \(M'(-2; 1)\) và

\(A'(-4; 4)\). Vẽ đồ thị: xem hình bên dưới.

Bài 8 trang 38 sgk Toán 9 tập 2

Bài 8. Biết rằng đường cong trong hình 11 là một parabol \(y = a{x^2}\).

a) Tìm hệ số \(a\).

b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x = -3\).

c) Tìm các điểm thuộc parabol có tung độ \(y = 8\).

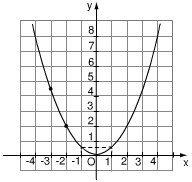
Bài giải:

a) Theo hình vẽ, ta lấy điểm \(A\) thuộc đồ thị có tọa độ là \(x = -2, y = 2\). Khi đó ta được:

 \(2 = a.{( - 2)^2} \Leftrightarrow a = {1 \over 2}\)

b) Đồ thị có hàm số là \(y = {1 \over 2}{x^2}\). Tung độ của điểm thuộc parabol có hoành độ \(x = -3\) là \(y = {1 \over 2}{( - 3)^2} = {9 \over 2}\).

c) Các điểm thuộc parabol có tung độ là \(8\) là:

\(8 = {1 \over 2}{x^2} \Leftrightarrow {x^2} = 16 \Leftrightarrow x =  \pm 4\)

Ta được hai điểm và tọa độ của hai điểm đó là \(M(4; 8)\) và \(M'(-4; 8)\).

Bài 9 trang 39 sgk Toán 9 tập 2

Bài 9. Cho hai hàm số \(y = {1 \over 3}{x^2}\) và \(y = -x + 6\).

a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ các giao điểm của hai đồ thị đó.

Bài giải:

*Vẽ đồ thị: \(y = {1 \over 3}{x^2}\)

*Vẽ đồ thị: \(y = -x + 6\)

- Cho \(x = 0 => y = 6\).

- Cho \(y = 0 => x = 6\).

Vẽ đồ thị: xem hình bên dưới.

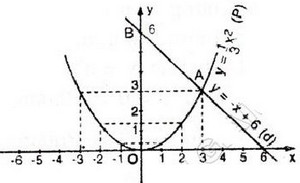
b) Giá trị gần đúng của tọa độ câc giao điểm (thực ra đây là giá trị đúng).

Hai đồ thị cắt nhau tại hai điểm \(A\) và \(B\).

Theo đồ thị ta có \(A(3; 3)\) và \(B(-6; 12)\).

Bài 10 trang 39 sgk Toán 9 tập 2

Bài 10. Cho hàm số \(y =  - 0.75{x^2}\). Qua đồ thị của hàm số đó, hãy cho biết khi \(x\) tăng từ \(-2\) đến \(4\) thì giá trị nhỏ nhất và giá trị lớn nhất của \(y\) là bao nhiêu ?

Bài giải:

Vẽ đồ thị: \(y =  - 0.75{x^2}\)

Do đó khi \(-2 ≤ x ≤ 4\) thì giá trị nhỏ nhất của hàm số là \(-12\) còn giá trị lớn nhất là \(0\).Vì \(-2 < 0 < 4\) và khi \(x = 0\) thì \(y = 0\) là giá trị lớn nhất của hàm số. Hơn nữa khi \(x = -2\) thì \(y =  - 0.75{( - 2)^2} =  - 3\), khi \(x = 4\) thì  \(y =  - 0.75{( 4)^2} =  -12<-3\).

Giaibaitap.me