Bài 69 trang 95 sgk Toán lớp 9 tập 2

Bài 69. Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh xe sau có đường kính \(1,672 m\) và bánh xe trước có đường kính là \(88cm\). Hỏi khi bánh xe sau lăn được \(10\) vòng thì bánh xe trước lăn được mấy vòng?

Hướng dẫn giải:

Chu vi bánh xe sau: \(π. 1,672\) (m)

Chu vi bánh xe trước: \(π . 0,88\) (m)

Khi bánh xe sau lăn được \(10\) vòng thì quãng đường đi được là:

                   \(π . 16,72\) (m)

Khi đó số vòng lăn của bánh xe trước là:

                   \(\frac{\pi .16,72}{\pi .0,88}\) = \(19\) vòng

Bài 70 trang 95 sgk Toán lớp 9 tập 2

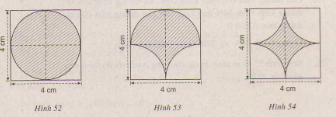
Bài 70. Vẽ lại ba hình (tạo bởi các cung tròn) dưới đây và tính chu vi mỗi hình (có gạch chéo)

Hướng dẫn giải:

Cách vẽ:

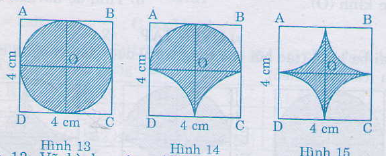
- Hình 13: Vẽ hình vuông \(ABCD\) cạnh \(4 cm\). Vẽ hai đường trung trực của các cạnh hình vuông, chúng cắt nhau tại \(O\).

Lấy \(O\) làm tâm vẽ đường tròn bán kính \(2cm\) ta được hình a.

- Hình 14: Vẽ hình vuông như hình a. Lấy \(O\) làm tâm vẽ nửa đường tròn bán kính \(2 cm\) tiếp xúc với các cạnh \(AB, AD, BC\). Lấy \(C, D\) làm tâm vẽ cung phần tư đường tròn về phía trong hình vuông các cung tròn đã vẽ tạo nên hình b .

- Hình 15: Vẽ hình vuông như hình a. Lấy \(A,B,C,D\) làm tâm vẽ về phía trong hình vuông bốn cung tròn, mỗi cung là phần tư đường tròn. Bốn cung này tạo nên hình c.

Tính chu vi mỗi hình:

- Hình 13: Đường kính đường tròn này là \(4 cm\).

Vậy hình tròn có chu vi là: \(3,14 . 4 = 12,56\) \((cm)\).

- Hình 14: Hình tròn gồnm hai cung: một cung là nửa đường tròn, hai cung có mỗi cung là phần tư đường tròn nên chu vi hình bằng chu vi của hình tròn ở hình a, tức là \(12,56\) \(cm\).

- Hình 15: Hình gồm bốn cung tròn với mỗi cung tròn là phần tư đường tròn nên chu vi hình bằng chu vi hình tròn ở hình a tức là \(12,56 cm\).

Bài 71 trang 96 sgk Toán lớp 9 tập 2

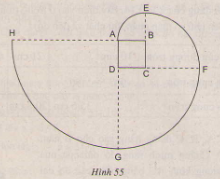
Bài 71. Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là \(B, C, D, A\) theo đúng kích thước đã cho (hình vuông \(ABCD\) dài \(1cm\) ). Nếu cách vẽ đường xoắn \(AEFGH\). Tính độ dài đường xoắn đó.

Hướng dẫn giải:

Cách vẽ: Vẽ hình vuông \(ABCD\) có cạnh dài \(1cm\).

Vẽ \(\frac{1}{4}\) đường tròn tâm \(B\), bán kính \(1\) cm, ta có cung \(\overparen{AE}\)

Vẽ \(\frac{1}{4}\) đường tròn tâm C, bán kính 2 cm, ta có cung \(\overparen{EF}\)

Vẽ \(\frac{1}{4}\) đường tròn tâm D, bán kính 3 cm, ta có cung \(\overparen{FG}\)

Vẽ \(\frac{1}{4}\) đường tròn tâm A, bán kính 4 cm, ta có cung \(\overparen{GH}\)

Độ dài đường xoắn:

               \({l_\overparen{AE}}\)= \(\frac{1}{4}\) . \(2π.1\)

               \({l_\overparen{EF}}\)= \(\frac{1}{4}\) . \(2π.2\)

               \({l_\overparen{FG}}\)= \(\frac{1}{4}\) . \(2π.3\)

               \({l_\overparen{GH}}\)= \(\frac{1}{4}\) . \(2π.4\)

Vậy: Độ dài đường xoắn là:

\({l_\overparen{AE}}\)+\({l_\overparen{EF}}\)+\({l_\overparen{FG}}\)+\({l_\overparen{GH}}\)= \(\frac{1}{4}\) .\( 2π (1+2+3+4) = 5π\)

Bài 72 trang 96 sgk Toán lớp 9 tập 2

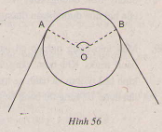
Bài 72. Bánh xe của một ròng rọc có chu vi là \(540mm\). Dây cua-roa bao bánh xe theo cung \(AB\) có độ dài \(200mm\). Tính góc \(AOB\) (h.56)

Hướng dẫn giải:

\(360^0\) ứng với \(540mm\).

\(x^0\) ứng với \(200mm\).

\(x\) = \(\frac{360. 200}{540}\) \(≈ 133^0\)  

Vậy \(sđ\overparen{AB} ≈ 133^0\), suy ra \(\widehat{AOB}\) \(≈ 133^0\)

Giaibaitap.me