Bài 65 trang 94 sgk Toán lớp 9 tập 2
Bài 65. Lấy giá trị gần đúng của \(π\) là \(3,14\), hãy điền vào ô trống trong bảng sau (đơn vị độ dài:\(cm\), làm tròn kết quả đến chữ thập phân thứ hai).

Giải

Từ \(C = 2πR\) \( \Rightarrow R = \)\(\frac{C}{2\pi }\); \(C = πd \) \(\Rightarrow d= \)\(\frac{C}{\pi }\).
Vậy dùng các công thức trên để tìm các giá trị chưa biết trong ô trống. Ta điền vào bảng sau:
Bài 66 trang 95 sgk Toán lớp 9 tập 2
Bài 66.
a) Tính độ dài cung \(60^0\) của mộ đường tròn có bán kính \(2 dm\).
b) Tính chu vi vành xe đạp có đường kính \(650mm\).
Hướng dẫn giải:
a) Áp dụng số vào công thức \(l = {{\pi Rn} \over {180}}\) ta có:
\(l = {{3,14.2.60} \over {180}}\) =\( 2,09 (dm) ≈ 21 (cm)\)
b) Độ dài vành xe đạp là: \(3,14. 650 = 2041 (mm) ≈ 2(m)\)
Bài 67 trang 95 sgk Toán lớp 9 tập 2
Bài 67. Lấy giá trị gần đúng của \(π\) là \(3,14\), hãy điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhất và đến độ):
Hướng dẫn giải:

Vận dụng công thức: \(l\) = \(\frac{\pi Rn}{180}\) để tìm \(R\) hoặc \(n^0\) hoặc l. Thay số vào, tính toán ta tìm được các giá trị chưa biết trong ô trống và điền vào bảng sau:

Bài 68 trang 95 sgk Toán lớp 9 tập 2
Bài 68. Cho ba điểm \(A, B, C\) thẳng hàng sao cho \(B\) nằm giữa \(A\) và \(C\). Chứng minh rằng độ dài của nửa đường tròn đường kính \(AC\) bằng tổng các độ dài của hai nửa đường tròn đường kính \(AB\) và \(BC\).
Hướng dẫn giải:
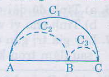
Gọi \({C_1},{C_2},{C_3}\) lần lượt là độ dài của các nửa đường tròn đường kính \(AC, AB, BC\), ta có:
\({C_1}\) = \(π. AC\) (1)
\({C_2}\) = \(π.AB\) (2)
\({C_3}\) = \(π.BC \) (3)
So sánh (1), (2), (3) ta thấy:
\({C_2} + {C_3} = \pi (AB + BC) = \pi AC\)
Vậy \({C_1} = {C_2} + {C_3}\).
Giaibaitap.me
Giải bài tập trang 95, 96 bài 9 độ dài đường tròn, cung tròn SGK Toán lớp 9 tập 2. Câu 69: Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước...
Giải bài tập trang 96 bài 9 độ dài đường tròn, cung tròn SGK Toán lớp 9 tập 2. Câu 73: Đường tròn lớn của Trái Đất dài khoảng...
Giải bài tập trang 98 bài 10 diện tích hình tròn, hình quạt tròn SGK Toán lớp 9 tập 2. Câu 77: Tính diện tích hình tròn nội tiếp một hình vuông cạnh là...
Giải bài tập trang 99, 100 bài 10 diện tích hình tròn, hình quạt tròn SGK Toán lớp 9 tập 2. Câu 84: Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh...
