Bài 53 trang 89 sgk Toán lớp 9 tập 2

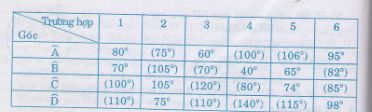
Bài 53. Biết \(ABCD\) là tứ giác nội tiếp. Hãy điền vào ô trống trong bẳng sau (nếu có thể)

Hướng dẫn giải:

- Trường hợp 1:

Ta có \(\widehat{A}\) + \(\widehat{C}\) = \(180^0\) => \(\widehat{C}\) = \(180^0\) - \(\widehat{A}\)= \(180^0\)– \(80^0\)=\(100^0\)

         \(\widehat{B}\) + \(\widehat{D}\) = \(180^0\) => \(\widehat{D}\) = \(180^0\)  - \(\widehat{B}\)= \(180^0\) – \(70^0\) = \(110^0\)

Vậy điểm \(\widehat{C}\) = \(100^0\) , \(\widehat{D}\)  = \(110^0\)

- Trường hợp 2:

Ta có  \(\widehat{A}\) + \(\widehat{C}\) = \(180^0\)=> \(\widehat{C}\) = \(180^0\) - \(\widehat{A}\)= \(180^0\)– \(105^0\)= \(75^0\)

         \(\widehat{B}\) + \(\widehat{D}\) =  \(180^0\) => \(\widehat{D}\) = \(180^0\) - \(\widehat{B}\)= \(180^0\) – \(75^0\) = \(105^0\)

- Trường hợp 3:

\(\widehat{A}\) + \(\widehat{C}\) = \(180^0\)=> \(\widehat{C}\) = \(180^0\)- \(\widehat{A}\)= \(180^0\) – \(60^0\) =\(120^0\)

 \(\widehat{B}\) + \(\widehat{D}\) =  \(180^0\) Chẳng hạn chọn \(\widehat{B}\)= \(70^0\),\(\widehat{D}\) = \(110^0\)

- Trường hợp 4: \(\widehat{D}\) = \(180^0\)- \(\widehat{B}\)= \(180^0\) – \(40^0\)= \(140^0\)

Còn lại \(\widehat{A}\) + \(\widehat{C}\) = \(180^0\). Chẳng hạn chọn \(\widehat{A}\)= \(100^0\) ,\(\widehat{B}\) =\(80^0\)

-   Trường hợp 5:  \(\widehat{A}\) = \(180^0\)- \(\widehat{C}\)=\(180^0\) – \(74^0\)= \(106^0\)

                         \(\widehat{B}\) = \(180^0\)  - \(\widehat{D}\)= \(180^0\) – \(65^0\)= \(115^0\)

-  Trường hợp 6: \(\widehat{C}\) = \(180^0\)  - \(\widehat{A}\)= \(180^0\) – \(95^0\) = \(85^0\)

                        \(\widehat{B}\) = \(180^0\)  - \(\widehat{D}\)=\(180^0\) – \(98^0\) = \(82^0\)

Vậy điền vào ô trống ta được bảng sau:

Bài 54 trang 89 sgk Toán lớp 9 tập 2

Bài 54. Tứ giác \(ABCD\) có \(\widehat{ABC}\) + \(\widehat{ADC}\) = \(180^0\). Chứng minh rằng các đường trung trực của \(AC, BD, AB\) cùng đi qua một điểm.

Hướng dẫn giải:

Tứ giác \(ABCD\) có tổng hai góc đối diện bằng \(180^0\) nên nội tiếp đường tròn tâm \(O\), ta có 

                  \(OA = OB = OC = OD\)

Do đó các đường trung trực của \(AB, BD, AB\) cùng đi qua \(O\)

Bài 55 trang 89 sgk Toán lớp 9 tập 2

Bài 55. Cho \(ABCD\) là một tứ giác nội tiếp đường tròn tâm \(M\), biết \(\widehat {DAB}\)= \(80^0\), \(\widehat {DAM}\) = \(30^0\), \(\widehat {BMC}\)= \(70^0\).

Hãy tính số đo các góc \(\widehat {MAB}\), \(\widehat {BCM}\), \(\widehat {AMB}\), \(\widehat {DMC}\), \(\widehat {AMD}\), \(\widehat {MCD}\) và \(\widehat {BCD}\)

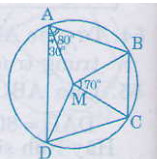
Ta có: \(\widehat {MAB} = \widehat {DAB} - \widehat {DAM} = {80^0} - {30^0} = {50^0}\) (1)

- \(∆MBC\) là tam giác cân (\(MB= MC\)) nên \(\widehat {BCM} = {{{{180}^0} - {{70}^0}} \over 2} = {55^0}\) (2)

- \(∆MAB\) là tam giác cân (\(MA=MB\)) nên \(\widehat {MAB} = {50^0}\) (theo (1))

Vậy \(\widehat {AMB} = {180^0} - {2.50^0} = {80^0}\)

 \(\widehat {BAD}\) =\(\frac{sđ\overparen{BCD}}{2}\)(số đo góc nội tiếp bằng nửa số đo của cung bị chắn)

\(=>sđ\overparen{BCD}\)=\(2.\widehat {BAD} = {2.80^0} = {160^0}\)  

Mà \(sđ\overparen{BC}\)= \(\widehat {BMC} = {70^0}\) (số đo ở tâm bằng số đo cung bị chắn)

Vậy \(sđ\overparen{DC}\)=\({160^0} - {70^0} = {90^0}\) (vì C nằm trên cung nhỏ cung \(BD\))

Suy ra \(\widehat {DMC} = {90^0}\)                    ⁽⁴⁾

\(∆MAD\) là tam giác cân (\(MA= MD\))

Suy ra \(\widehat {AMD} = {180^0} - {2.30^0}\)   (5)

\(∆MCD\) là tam giác vuông cân (\(MC= MD\)) và \(\widehat {DMC} = {90^0}\)

Suy ra \(\widehat {MCD} = \widehat {MDC} = {45^0}\)  (6)

\(\widehat {BCD} = {100^0}\) theo (2) và (6) và vì CM là tia nằm giữa hai tia \(CB, CD\).

Bài 56 trang 89 sgk Toán lớp 9 tập 2

Bài 56. Xem hình 47. Hãy tìm số đo các góc của tứ giác \(ABCD\)

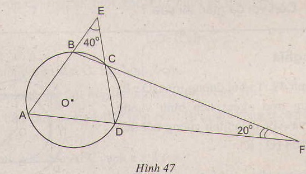
Hướng dẫn giải:

Ta có \(\widehat{BCE}\) = \(\widehat{DCF}\) (hai góc đối đỉnh)

Đặt \(x\) = \(\widehat{BCE}\) = \(\widehat{DCF}\). Theo tính chất góc ngoài tam giác, ta có:

      \(\widehat{ABC}\) = \(x\) +  \(40^0\)       (1)

      \(\widehat{ADC}\) = \(x\) +  \(20^0\)           (2)

Lại có \(\widehat{ABC}\) +\(\widehat{ADC}\) =   \(180^0\)    (3)

(hai góc đối diện tứ giác nội tiếp)

Từ (1), (2), (3) suy ra:

              \(180^0\)  = \(2x\) + \(60^0\)   \(\Rightarrow\) \(x \)= \(60^0\)  

Từ (1), ta có:

              \(\widehat{ABC}\) = \(60^0\)   + \(40^0\)   = \(100^0\)  

Từ (2), ta có:

             \(\widehat{ADC}\) = \(60^0\)  +\(20^0\)   = \(80^0\)  

\(\widehat{BCD}\) = \(180^0\)   \(–  x\) (hai góc kề bù)

\(\Rightarrow\)\(\widehat{BCD}\) = \(120^0\)  

\(\widehat{BAD}\) = \(180^0\)  - \(\widehat{BCD}\) (hai góc đối diện của tứ giác nội tiếp)

\(\Rightarrow\) \(\widehat{BAD}\) = \(180^0\)– \(120^0\) = \(60^0\)

Giaibaitap.me