Bài 40 trang 27 SGK Toán 9 tập 2

Giải các hệ phương trình sau và minh họa hình học kết quả tìm được:

a)\(\left\{ \matrix{2{\rm{x}} + 5y = 2 \hfill \cr {2 \over 5}x + y = 1 \hfill \cr} \right.\)

b) \(\left\{ \matrix{0,2{\rm{x}} + 0,1y = 0,3 \hfill \cr 3{\rm{x}} + y = 5 \hfill \cr} \right.\)

c) \(\left\{ \matrix{{3 \over 2}x - y = {1 \over 2} \hfill \cr 3{\rm{x}} - 2y = 1 \hfill \cr} \right.\)

Giải

a) Giải hệ phương trình: 

\(\left\{ \matrix{
2{\rm{x}} + 5y = 2(1) \hfill \cr
{2 \over 5}x + y = 1(2) \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2{\rm{x}} + 5y = 2(1') \hfill \cr
- 2{\rm{x}} - 5y = - 5(2') \hfill \cr} \right.\)

Cộng (1’) với (2’) vế theo vế, ta được: \(0x + 0y = -3\)

Phương trình này vô nghiệm. Vậy hệ đã cho vô nghiệm.

Minh họa hình học kết quả tìm được:

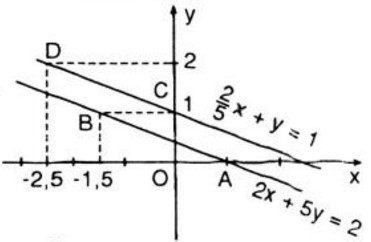
- Vẽ đồ thị hàm số \(2x + 5y = 2\).

Cho \(y = 0 ⇒  x = 1\). Ta xác định được điểm \(A(1; 0)\)

Cho \(y = 1 ⇒ x = -1,5\). Ta xác định được điểm \(B(-1,5; 1)\).

Đồ thị hàm số là đường thẳng đi qua hai điểm A và B

-Vẽ đồ thị hàm số  \({2 \over 5}x + y = 1 \Leftrightarrow 2{\rm{x}} + 5y = 5\)

Cho \(x = 0 ⇒ y = 1\). Ta xác định được điểm \(C(0; 1)\)

Cho \(y = 2 ⇒ x = -2,5\). Ta xác định được điểm \(D(-2,5; 2)\)

Đồ thị hàm số là đường thẳng đi qua hai điểm C và D.

Kết luận: Đồ thị hai hàm số trên song song. Điều này chứng tỏ rằng hệ phương trình vô nghiệm.

b) Giải hệ phương trình:  

\(\left\{ \matrix{
0,2{\rm{x}} + 0,1y = 0,3(1) \hfill \cr
3{\rm{x}} + y = 5(2) \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 2{\rm{x}} - y = - 3(1') \hfill \cr
3{\rm{x}} + y = 5(2') \hfill \cr} \right.\)

Cộng (1’) với (2’) vế theo vế, ta được \(x = 2\)

Thế \(x = 2\) vào (2), ta được: \(6 + y = 5 ⇔ y = -1\)

Vậy nghiệm của hệ phương trình là \((x = 2; y = -1)\)

Minh họa hình học:

- Đồ thị hàm số \(0,2x + 0,1y = 0,3\) là một đường thẳng đi qua hai điểm:

\(A(x = 0; y = 3)\) và \(B(x = 1,5; y = 0)\)

- Đồ thị hàm số \(3x + y = 5\) là một đường thẳng đi qua hai điểm \(C(x = 0; y = 5)\) và \(D(x = 1; y = 2)\)

- Đồ thị hai hàm số trên cắt nhau tại điểm: \(M(x = 2; y = -1)\).

Vậy \((2; -1)\) là một nghiệm của hệ phương trình.

c) Giải hệ phương trình:

\(\left\{ \matrix{
{3 \over 2}x - y = {1 \over 2}(1) \hfill \cr
3{\rm{x}} - 2y = 1(2) \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 3{\rm{x}} + 2y = - 1(1') \hfill \cr
3{\rm{x}} - 2y = 1(2') \hfill \cr} \right.\)

Cộng (1’) và (2’) vế theo vế, ta có: \(0x + 0y = 0\).

Phương trình này có vô số nghiệm.

Nghiệm tổng quát là \(\left( {x;{3 \over 2}x - {1 \over 2}} \right)\)  với \(x ∈ R\)

Minh họa hình học

- Đồ thị hàm số (1) là đường thẳng đi qua hai điểm \(A(0;  - {1 \over 2})\) và \(B(1;1)\) nên hai đường thẳng này trùng nhau. Vậy hệ phương trinh có vô số nghiệm.

Bài 41 trang 27 SGK Toán 9 tập 2

Giải các hệ phương trình sau:

a) 

\(\left\{ \matrix{
x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1 \hfill \cr
\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1 \hfill \cr} \right.\)

b)  

\(\left\{ \matrix{
{{2{\rm{x}}} \over {x + 1}} + {y \over {y + 1}} = \sqrt 2 \hfill \cr
{x \over {x + 1}} + {{3y} \over {y + 1}} = - 1 \hfill \cr} \right.\)

Giải:

a) 

\(\left\{ \matrix{
x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1(1) \hfill \cr
\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1(2) \hfill \cr} \right.\)

Ta giải hệ phương trình bằng phương pháp thế:

Từ (1) ta có  \(x = {{\left( {1 + \sqrt 3 } \right)y + 1} \over {\sqrt 5 }}(3)\)

Thế (3) vào (2), ta được:  

\(\eqalign{
& \left( {1 - \sqrt 3 } \right)\left[ {{{\left( {1 + \sqrt 3 } \right)y + 1} \over {\sqrt 5 }}} \right] + y\sqrt 5 = 1 \cr
& \Leftrightarrow \left( {1 - \sqrt 3 } \right)\left( {1 + \sqrt 3 } \right)y + \left( {1 - \sqrt 3 } \right) + 5y = \sqrt 5 \cr
& \Leftrightarrow - 2y + 5y = \sqrt 5 + \sqrt 3 - 1 \Leftrightarrow y = {{\sqrt 5 + \sqrt 3 - 1} \over 3} \cr} \)

Thế y vừa tìm được vào (3), ta được:

\(x = {{\left( {1 + \sqrt 3 } \right)\left( {{{\sqrt 5  + \sqrt 3  - 1} \over 3}} \right) + 1} \over {\sqrt 5 }}\) hay  \(x = {{\sqrt 5  + \sqrt 3  + 1} \over 3}\)

Vậy hệ phương trình có nghiệm là: \(\left( {{{\sqrt 5  + \sqrt 3  + 1} \over 3};{{\sqrt 5  + \sqrt 3  - 1} \over 3}} \right)\)

b)Giải hệ phương trình: (I) 

\(\left\{ \matrix{
{{2{\rm{x}}} \over {x + 1}} + {y \over {y + 1}} = \sqrt 2 \hfill \cr
{x \over {x + 1}} + {{3y} \over {y + 1}} = - 1 \hfill \cr} \right.\)

Ta giải hệ phương trình bằng phương pháp đặt ẩn phụ.

Đặt \(u = {x \over {x + 1}};v = {y \over {y + 1}}\)

Thay vào hệ (I), ta có hệ mới với ẩn là \(u\) và \(v\) ta được:

\(\left\{ \matrix{
2u + v = \sqrt 2 (1') \hfill \cr
u + 3v = - 1(2') \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2u + v = \sqrt 2 (3) \hfill \cr
- 2u - 6v = 2(4) \hfill \cr} \right.\)

Cộng (3) và (4) vế theo vế, ta được: \( - 5{\rm{v}} = 2 + \sqrt 2  \Leftrightarrow v = {{ - \left( {2 + \sqrt 2 } \right)} \over 5}\)

Thay \(v = {{ - \left( {2 + \sqrt 2 } \right)} \over 5}\) vào (1’), ta được:

\(2u = {{2 + \sqrt 2 } \over 5} + \sqrt 2  \Leftrightarrow 2u = {{2 + \sqrt 2  + 5\sqrt 2 } \over 5} = {{2 + 6\sqrt 2 } \over 5}\)

\(\Leftrightarrow u = {{1 + 3\sqrt 2 } \over 5}\)

Với giá trị của \(u,v\) vừa tìm được, ta thế vào để tìm nghiệm \(x, y\).

Ta có: 

\(\left\{ \matrix{
{x \over {x + 1}} = {{1 + 3\sqrt 2 } \over 5} \hfill \cr
{y \over {y + 1}} = {{ - 2 - \sqrt 2 } \over 5} \hfill \cr} \right.đk\left\{ \matrix{
x \ne - 1 \hfill \cr
y \ne - 1 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{
x = \left( {x + 1} \right)\left( {{{1 + 3\sqrt 2 } \over 5}} \right) \hfill \cr
y = \left( {y + 1} \right){{\left( { - 2 - \sqrt 2 } \right)} \over 5} \hfill \cr} \right.\)

\(\left\{ \matrix{
5{\rm{x}} = \left( {x + 1} \right)\left( {1 + 3\sqrt 2 } \right) \hfill \cr
5y = \left( {y + 1} \right)\left( { - 2 - \sqrt 2 } \right) \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = {{1 + 3\sqrt 2 } \over {4 - 3\sqrt 2 }} \hfill \cr
y = {{-2 - \sqrt 2 } \over {7 + \sqrt 2 }} \hfill \cr} \right.\)

Vậy nghiệm của hệ phương trình là: \(\left( {{{1 + 3\sqrt 2 } \over {4 - 3\sqrt 2 }};{{-2 - \sqrt 2 } \over {7 + \sqrt 2 }}} \right)\) thỏa mãn điều kiện

Bài 42 trang 27 SGK Toán 9 tập 2

Giải hệ phương trình\(\left\{ \matrix{2{\rm{x}} - y = m \hfill \cr 4{\rm{x}} - {m^2}y = 2\sqrt 2 \hfill \cr} \right.\) trong mỗi trường hợp sau:

a) \(m = -\sqrt{2}\)       b) \(m = \sqrt{2}\)        c) \(m = 1\)

Giải:

(I) \(\left\{ \matrix{2{\rm{x}} - y = m(1) \hfill \cr 4{\rm{x}} - {m^2}y = 2\sqrt 2 (2) \hfill \cr} \right.\)

Ta có (1) ⇔ \(y = 2x – m\) (3)

Thế (3) vào (2), ta có:

\(4{\rm{x}} - {m^2}\left( {2{\rm{x}} - m} \right) = 2\sqrt 2\)

\( \Leftrightarrow 2\left( {2 - {m^2}} \right)x = 2\sqrt 2  - {m^3}(*)\) 

a) Với \(m = - \sqrt{2}\). Thế vào phương trình (*), ta được:

\(2(2 – 2)x = 2\sqrt{2} + 2\sqrt{2} ⇔ 0x = 4\sqrt{2}\)

Vậy hệ phương trình đã cho vô nghiệm.

b) Với \(m = \sqrt{2}\). Thế vào phương trình (*), ta được:

\(2(2 – 2)x = 2\sqrt{2} - 2\sqrt{2} ⇔ 0x = 0\)

Vậy hệ trình này có vô số nghiệm.

c) Với \(m = 1\). Thế vào phương trình (*), ta được:

\(2.(2-1)x = 2\sqrt 2  - 1 \Leftrightarrow 2{\rm{x}} = 2\sqrt 2  - 1\)

\(\Leftrightarrow x = {{2\sqrt 2  - 1} \over 2}\) 

Thay \(x\) vừa tìm được vào (3), ta có: \(y = 2\sqrt{2} – 2\)

Vậy hệ phương trình có một nghiệm duy nhất là: \(\left( {{{2\sqrt 2  - 1} \over 2};2\sqrt 2  - 2} \right)\)

Bài 43 trang 27 SGK Toán 9 tập 2

Bài 43. Hai người ở hai địa điểm A và B cách nhau 3,6 km, khởi hành cùng một lúc, đi ngược chiều nhau và gặp nhau ở một địa điểm cách A là 2 km. Nếu cả hai cùng giữ nguyên vận tốc như trường hợp trên, nhưng người đi chậm hơn xuất phát trước người kia 6 phút thì họ sẽ gặp nhau ở chính giữa quãng đường. Tính vận tốc của mỗi người.

Giải:

Gọi \(x\) (m/phút) là vận tốc của người xuất phát từ A và \(y\) (m/phút) là vận tốc của người xuất phát từ B.

Điều kiện: \(x > 0; y > 0\)

- Khi gặp nhau tại điểm cách A là 2km thì người xuất phát từ A đi được 2000 mét, còn người xuất phát từ B đi được 1600 mét.

Ta có phương trình: \({{2000} \over x} = {{1600} \over y}(1)\) 

- Theo đề bài cho thấy người xuất phát từ B đi chậm hơn. Khi người đi từ B xuất phát trước người kia 6 phút thì hai người gặp nhau ở chính giữa quãng đường, nghĩa là mỗi người đi được 1,8km = 1800m.

Ta có phương trình \({{1800} \over x} + 6 = {{1800} \over y}(2)\) 

Ta có hệ phương trình: (I) \(\left\{ \matrix{{{2000} \over x} = {{1600} \over y}(1) \hfill \cr {{1800} \over x} + 6 = {{1800} \over y}(2) \hfill \cr} \right.\)

Đặt \(u = {{100} \over x}\) và \(v = {{100} \over y}\) . Thay vào (I), ta được:  

\(\left( I \right) \Leftrightarrow \left\{ \matrix{20u = 16v \hfill \cr 18u + 6 = 18v \hfill \cr} \right.\)

Giải hệ phương trình ta được \(u = {4 \over 3}\) và \(v = {5 \over 3}\) 

- Với \({{100} \over x} = u = {4 \over 3} \Leftrightarrow x = 75\) (nhận)

- Với \({{100} \over y} = v = {5 \over 3} \Leftrightarrow y = 60\) (nhận)

Vậy vận tốc của người đi từ A là 75m/phút và người đi từ B là 60m/phút.

Giaibaitap.me