Bài 4 trang 36 sgk Toán 9 tập 2

Bài 4. Cho hai hàm số: \(y = {3 \over 2}{x^2},y =  - {3 \over 2}{x^2}\). Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.

Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.

Bài giải:

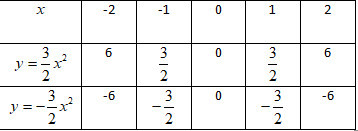
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:

Vẽ đồ thị:

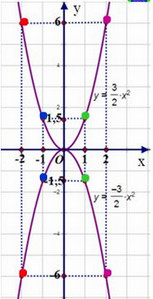
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.

Bài 5 trang 37 sgk Toán 9 tập 2

Bài 5. Cho ba hàm số:

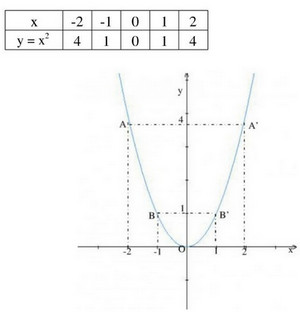
\(y = {1 \over 2}{x^2};y = {x^2};y = 2{x^2}\)

a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm ba điểm \(A, B, C\) có cùng hoành độ \(x = -1,5\) theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.

c) Tìm ba điểm \(A', B', C'\) có cùng hoành độ \(x = 1,5\) theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A', B và B', C và C'.

d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.

Bài giải:

a) Vẽ đồ thị

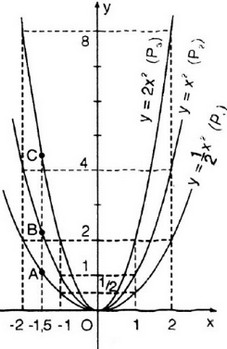
b) Gọi \({y_A},{y_B},{y_C}\) lần lượt là tung độ các điểm \(A, B, C\) có cùng hoành độ \(x = -1,5\). Ta có:

\(\eqalign{
& {y_A} = {1 \over 2}{( - 1,5)^2} = {1 \over 2}.2,25 = 1,125 \cr
& {y_B} = {( - 1,5)^2} = 2,25 \cr
& {y_C} = 2{( - 1.5)^2} = 2.2,25 = 4,5 \cr} \)

c) Gọi \({y_{A'}},{y_{B'}},{y_{C'}}\)  lần lượt là tung độ các điểm \(A', B', C'\) có cùng hoành độ \(x = 1,5\). Ta có:

\(\eqalign{
& {y_{A'}} = {1 \over 2}{(1,5)^2} = {1 \over 2}.2,25 = 1,125 \cr
& {y_{B'}} = {(1,5)^2} = 2,25 \cr
& {y_{C'}} = 2{(1.5)^2} = 2.2,25 = 4,5 \cr} \)

Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.

d) Với mỗi hàm số đã cho ta đều có hệ số \(a > 0\) nên O là điểm thấp nhất của đồ thị.

Vậy \(x = 0\) thì hàm số có giả trị nhỏ nhất.

Bài 6 trang 38 sgk Toán 9 tập 2

Bài 6. Cho hàm số \(y = f(x) = {x^2}\).

a) Vẽ đồ thị của hàm số đó.

b) Tính các giá trị \(f(-8); f(-1,3); f(-0,75); f(1,5)\).

c) Dùng đồ thị để ước lượng các giá trị \({(0,5)^2};{( - 1,5)^2};{(2,5)^2}\).

d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số \(\sqrt{3}; \sqrt{7}\).

Bài giải:

a) Vẽ đồ thị hàm số y = x². 

b) Ta có \(y = f(x) = {x^2}\) nên

\(\eqalign{
& f\left( { - 8} \right){\rm{ }} = {\rm{ }}{\left( { - 8} \right)^2} = {\rm{ }}64;{\rm{ }}f\left( { - 1,3} \right){\rm{ }} = {\rm{ }}{\left( { - 1,3} \right)^2} = {\rm{ }}1,69;{\rm{ }} \cr
& f\left( { - 0,75} \right){\rm{ }} = {\rm{ }}{\left( { - 0,75} \right)^2} = {\rm{ }}0,5625; \cr
& {\rm{ }}f\left( {1,5} \right){\rm{ }} = {\rm{ }}1,{5^2} = {\rm{ }}2,25 \cr} \)

c) Theo đồ thị ta có:

\(\eqalign{
& {(0,5)^2} \approx 0,25 \cr
& {( - 1,5)^2} \approx 2,25 \cr
& {(2,5)^2} \approx 6,25 \cr} \)

d) Theo đồ thị ta có: Điểm trên trục hoành \(\sqrt{3}\) thì có tung độ là \(y = {(\sqrt 3 )^2} = 3\). Suy ra điểm biểu diễn \(\sqrt{3}\) trên trục hoành bằng\( 1,7\). Tương tự điểm biểu diễn \(\sqrt{7}\) gồm bằng \(2,7\).

Giaibaitap.me